Заменим эту схему равнозначной схемой фиг. 4.541).

Так как оба контура совершенно симметричны, то возникшие в них колебания .будут совершенно одинаковыми. Направление токов в первый момент показано на фиг. 4.54. Легко видеть, что эти токи имеют одинаковое напранлёние в катушке связи.

Все величины, характеризующие колебания, определяются теми же уравнениями, как и для предыдущего сяучая, но только взамен (L - М) теперь станет (L-j-M).

Осуществим теперь оба способа возбуждения одновременно. Для этого надо верхней на чертеже обкладке конденсатора первого контура дважды

fL-M) (L-M)

Л Л ,-птг-J-птг

( L~M)

(L-M)

ЛЛЛАЛл

ЛЛЛЛЛг

-VWW-

ЛЛЛЛЛг

Фиг. 4.54.

Фиг. 4.5.

сообщить положительный заряд, а такой же обкладке конденсатора второго контура один раз сообщить отрицательный, а другой раз - равный ему положительный заряд.

В результате окажется, что заряжен только первый контур,-и притом до двойной амплитуды.

Из этого следует, что когда заряд в рассматриваемой двухконтурной системе начинается с того, что заряжен только первый конденса,тор до напряжений Ет, то течение процессов происхадит так, как будто одновременно были осуществлены оба предыдущих способа разряда.

ЛЛЛЛЛг

-ЛЛЛЛЛг

ЛЛЛЛЛг

-ЛЛЛЛЛг

Фиг. 4.5&.

Фиг. 4.57.

Таким образом, например, ток в первом контуре может рассматриваться, как сумма двух токов / и / . Первый из них соответствует разряду обоих конденсаторов с первоначальным расположением знаков согласно фиг. 4.56, а второй - согласно фиг. 4.57.

Совмещая в одной системе заряды, указанные на фиг. 4.56 и фиг. 4.57,

и обозначая теперь суммарный ток в первом контуре /j, запишем это так

А = / + /

) Чтобы технически осуществить рассматриваемый случай, делают искровой промежуток в цепи катушки связи (в точке А фиг. 4.55) и подводят сюда высокое напряжение. Когда проскакивает искра, промежуток А перекрывается, и схема становится равнозначной схеме фиг, 4.53,

Во втором контуре ток 1 имеет противоположное направление. Поэтому

Зная ток /а, легко перейти и к напряжению на конденсаторе второго контура 2, так как

/соС

Обратим внимание, что если первоначальный полный заряд на первом конденсаторе обозначить не 2Ет, а просто Ет, то в выражениях для амплитуд составляющих токов появится двойка в знаменателе.

Так например,

/ -Щте- (4-102)

Этим обозначением мы и будем дальще пользоваться.

§ 25. Случай, когда оба контура не имеют затухания.

На основании результатов, полученных в предыдущем параграфе, фас-смстрим случай, когда система состоит из двух одинаковых контуров без затухания (фиг. 4.58), причем при f = 0 в системе имеется только напряжение Ет на конденсаторе первого контура. fL-M) Будем пользоваться следующими

у-ууОТр-, обозначениями. Слагающий ток, соответствующий колебаниям первого типа

(L-M)

с частотой (01 =

, обозначаем

Фиг. 4.58.

V{L~M)C)

V или /.

Ток, соответствующий колебаниям

второго типа fс частотойш,====--=4==== \ , V(L-\-M)Cj.

обозначаем i или Те же индексы будем применять и для слагающих напряжений.

По;Ь1Ый ток в первом контуре или /j. Напряжение на конденсаторе

первого и второго контура e-i, Ё, и Е.

Выпишем формулы, определяющие значения токов

2.,(L-M) КО при >0 ~sin(io,t) при f>0

L = i - i

(4.10a)

V(L~M) С

T/(L + M)C

Из этих уравнений очевидно, что с момента t = 0 в каждом контуре существует два синусоидальных колебания с различными периодами.

Такие колебания дают, как известно, биения, причем период биений х равен разности между числом колебаний в секунду, так что

(4.104)

Полное напряжение на первом конденсаторе найдется умножением тока /j на емкостное сопротивление первого контура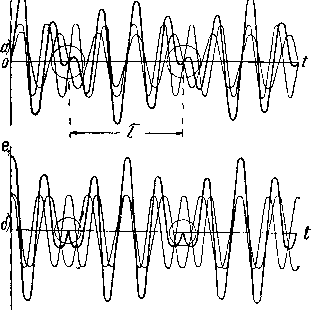

1 = 7

(4.105)

Так же для второго контура.

(4.106)

Фиг. 4.59.

Фиг. 4.60.

На фиг. 4.59 показан пример кривых, соответствующих данному случаю. На кривой а) тонкими линиями показаны слагающие токи в первом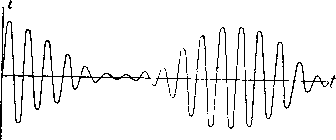

Фиг. 4.61.

контуре, а жирной линией их сумма. На кривых б) то же для напряжений в первом- контуре

) Характерным свойством этих кривых является поворот фазы колебания на 180° во время перехода через узел биения, как это отмечено на фиг. 4.59 кружками.

Для лучшего пояснения приводим еще фиг. 4.60, на которой пунктиром показано продолжение кривой, которое имело бы место, если бы не было поворота фазы. Таким образом кривая фиг. 4.61 не выражает собой биения между двумя коле0аниями, как это иногда ошибочно изображают. Такая кривая является суммой трех колебаний

А cos (cof) + cos [(со -Ь Д) П + cos - А)