Поэтому, исходя из- того, что при Х2 = 0 ур-ние (4.72) § 16 дает

ReRг-=Xs (4.74)

можно, приравняв сопротивление Re сопротивлению Ri, написать

/?1/?2 = Хз. (4.75)

Ур-ние (4.75), как известно, выражает собой условие критической связи между контурами.

Вследствие равенства полезного и вредного сопротивлений отдача равна 50/о.

Связь, соответствующая условию

RR=zX\

как было сказано, называется критической , кроме того, ее называют также оптимальной , связь больше оптимальной называется достаточной-или сильной, связь меньше оптимальной - слабой или недостаточной.

§ 18. Коэфициент полезного действия в случае достаточной связи.

Мы нашли, что кпд равен (ур-ние 4.70)

Далее мы установили, что при прочих равных условиях кпд наибольший при Х2 = 0, вследствие чего

Проследим, как изменяется кпд при условии, что оба контура настроены в резонанс (Xi = 0 и Хг -0).

Так как кпд растет с увеличением связи Xg и так как установлено, что он достигает 50 /о> когда эта связь становится критической (оптимальной), то очевидно, что при

Xg < RlR ,

Ъ <50о/о.

Делая связь больше критической, мы будем увеличивать кпд и можем сделать его сколь угодно большим.

Однако мощность во вторичном контуре, разумеется, будет падать, так как она равна (ур-ние 4.69)

а в свою очередь

R + Rs или

Отсюда видно, что с возрастанием вносимого сопротивления мощность во вторичном контуре падает.

Если начертить кривые изменения кпд и мощности в зависимости от связи, они получат вид фиг. 4.39.

Однако при связи 0олъше критической можно получить болыйую мощность, если контуры настроены не в резонанс. Действительно, прйГ резонансе согласно графику фиг. 4.38, § 13 мы находился в начале координат. Перестроив оба контура так, чтобы приблизиться к вершинам А и В, мы этим самым увеличим ток во вторичном контуре. Следствием этого будет то, что вносимое сопротивление и кпд уменьшатся.

Если настроить контуры так, чтобы оказаться на одной из вершин, то будем иметь, как известно,

Подставив это в ур-ние (4.71) § 16

Re =

л- Яг

получим

Rs R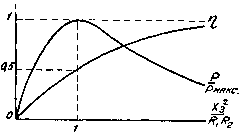

Фиг. 4.39.

т. е. то же условие, что и при оптимальной связи для Xi = О и Ха = 0.

В эгом случае так же, как и в случае оптимальной связи, эдс в первом контуре будет испытывать чисто активную нагрузку, равную IRx-

В промежуточных случаях нагрузка будет иметь реактивную составляющую.

Сопротивления контуров, взятых в отдельности, будут комплексными, причем при настройке, соответствующей точке В (фиг. 4.38) (или вблизи нее), контуры будут являться индуктивным сопротивлением, в точке А - емкостным.

На практике при передаче энергии посредством двухконтурной системы обычно работают в точке полного резонанса (Xi = 0, Х2 = 0). Если нужно передать во вторичный контур максимальную мощность, - связь делают оптимальной. - Если нужно получить высокий кпд, - связь делают выше оптимальной. И только в тех случаях, когда передача мощности и кпд играют второстепенный характер, и система используется в роли фильтра,- применяется связь меньше критической, вследствие чего сопротивление вносимое в первый контур, от нагрузки R уменьшается.

§ 19. Параллельное включение эдс.

(L-M)

До сих пор мы рассматривали случаи, когда эдс была включена в первый

контур последовательно. Положим теперь (фиг. 4.40), что эдс Е присоединена параллельно первому контуру, причем требуется найти условия, при которых вход]ое сопротивление первого контура чисто активное и равно заданной величине г.

Обозначим буквой / (без индекса) ток, идущий через источник. Если бы емкости Cl не было вовсе, прежние уравнения были бы применимы к данному случаю с оговоркой, что Xi = <o (Li-N1) и не может быть сделано равным нулю. Х2=0, что соответствует максимальному кпд, получим из

-vww- Фиг. 4.40.

-ЛЛЛЛЛг

Положив ур-ния (4.30)

(4.77)

Введем теперь емкость и дадим ей такую величину, чтобы мнимая составляющая тока обратилась в нуль. Для этого должно быть

ур-ние (4.78) определяет величину емкости, настраивающей первый контур таким образом, что его входное сопротивление для параллельной эдс.оказывается чисто активным, при условии, что второй контур настроен в резонанс с частотой со.

Величину входного сопротивления г легко определить из ур-ния (4.77), имея в виду, что мнимая асть равна нулю

г - (i2+X,g) + (XiRa)

При расчете контура величины и Xg должны быть выбраны такими, чтобы ур-ние (4.79) было удовлетворено при заданной величине г. Мощность, затрачиваемая источником,

Р=~ (4.80)

Мощность, выделяемая в сопротивлении R,

P2 = IiR- (4.81)

Кпд (при условии сделанных выще предпосылок)

- = n£f- (4.82)

§ 20. Полный коэфициент полезного действия.

Вторичный контур всегда обладает некоторым вредным сопротивлением. Этим вредным сопротивлением можно пренебречь, если полезное сопротивление, включенное последовательно с вредным, значительно больше него. Если это условие не имеет места, то сопротивление R надо разбить на две части: вредную R! и полезную i?./.

В этом случае полный коэфициент полезного действия будет

чполн, = (4.83)

а полезная мощность будет

2пслеги. - I R

Эта мощность разумеется максимальна в том случае, когда полная мощность, переходящая во второй контур, имеет Наибольшую величину, т. е. когда

R{R,JR,%

Полный коэфициент полезного действия, как ясно из ур-ния (4.83), всегда меньше 50 /о. Из этого следует, что сопротивление контура всегда надо делать по возможности малым по сравнению с сопротивлением нагрузки.

§ 21. Случай, когда вторичный контур не имеет конденсатора.

Часто встречаются устройства, в которых вторичный контур представляет собой катушку, связанную индуктивно с первичным контуром и питающую нагрузочное сопротивление ?2-