Эти уравнения показывают следующее.

Положим, что мы поставили конденсатор Cg в какое-то произвольное положение (т. е. задали некоторое значение) и изменяем конденсатор Cj (т. е. даем величине различные значения). Наблюдая изменение амплитуды тока 1т2, мы обнаружим максимум при

X, =

(4.52)

Это будет частный резонанс первого рода.

Если теперь изменить величину х, то ток может возрасти или уменьшиться в зависимости от того, какова была прежняя величина Хз и как она изменилась. Но во всяком случае теперь, снова изменяя Xi, мы найдем некоторое новое положение, при котором /2 достигает максимума, т. е. новый частный резонанс первого рода, соответствующий новому значению х. Если величина Xg была изменена произвольно, то амплитуда тока при этом новом положении резонанса может быть больше или меньше предыдущей в зависимости от обстоятельств. Но, если, найдя частный резонанс первого рода при некотором постоянном х, мы оставляем теперь неизменным х и при помощи конденсатора Cg находим максимум тока, то мы окажемся в положении резонанса второго рода, и амплитуда тока вообще будет больше предыдущей. Так, настраиваясь по очереди, мы достигаем, наконец, максимально возможного значения амплитуды тока.

Этому положению будет соответствовать одновременное удовлетворение как условия

так и условия

Хо =

х + Ri

xl + R\

(4.52)

(4.53)

Чтобы найти Хх и х, соответствующие такому положению, надо решить совместно ур-ния (4.52) и (4.53).

Сделав это, получим следующие три решения:

1) Xi==0; Х2 = 0

V ;(-л)

Xi = Ха

-R1R2)

(4.54) (4.55)

(4.56)

Таким образом в общем случае Существует три положения настройки, при которых изменение х при Х2 = const или изменение Xg при Xi = const приведет к уменьшению тока.

Первое положение называется положением полного резонанса, а второе и третье - положениями сложного резонанса.

Если связь меньше критической, т. е.

xf <С RjRzf

решения второе и третье делаются невозможными, так как х и получают мнимые значения.

Следовательно, при связи, меньшей, чем критическая, остается только одно положение полного резонанса

При связи, большей, чем критическая, все три положения резонанса существуют.

Подставив значения = О и Х2 = 0 в ур-ние (4.49), найдем

(4.57)

Подставив в то же >р-ние значения х и из ур-ний (4.55) и (4.56), получим

= --L=r. (4.58)

Сравнивая (4.57) и (4.58), видим, что в случае (4.58) амплитуда тока достигает большего значения, чем в случае (4.57). Эти значения сдановятся одинаковыми при

т. е. при таком устройстве цепи, когда связь как раз равна критической.

§ 13. Графическое изображение амплитуды вторичного тока.

Сложная картина, которая с количественной стороны была описана в предыдущем параграфе, может быть гораздо более ясно понята с качественной стороны при помощи графического изображения функций -р- -

= F (Xj, х}. Эта функция от двух независимых переменных, и поэтому она может быть изображена некоторой поверхностью. Для того чтобы передать поверхность при помощи чертежа, прибегают к способу, принятому в топографии, при котором точки с одинаковой высотой соединяются в одну общую линию, называемую гориз,онталью. Горизонтали проводятся через определенные интервалы высот и, будучи спроектированы на плоскость, дают С1стему кривых, на которых отмечена соответствующая им высота. Такая система с большой наглядностью выражает рельеф местности.

Густота горизонталей выражает крутизну скатов. Ямы и вершины окружены замкнутыми горизонталями, ложбины и мысовидные выступы характеризуются впадинами и выступами на горизонталях.

На фиг. 4.38 показано такое построение, выражающее зависимость Па от Xj и Xg. Диаграмма соответствует случаю R - l; i?2 = 2; Хз = 3. Горизонтальная линия, проведенная через середину чертежа, представляет собой ось, на которой отложены значения Xg. Вправо от точки О эти значения положительны, влево - отрицательны. Перпендикулярная линия представляет собой такую же ось для Xi.

Каждой комбинации Xi или х соответствует некоторая точка, высота которой под нулевым уровнем определяется горизонталями и выражает

собой в относительных единицах значение при данных Xi и Xg.

Изображенная поверхность имеет две вершины А и В. Вблизи этих вершин любое изменение х и Xg, или обоих одновременно, вызывает переход на более низкий уровень, т. е. уменьшение Jm2- Эти вершины соответствуют максимальному возможному значению амплитуды тока во вторичном контуре. Если стать в точке Xi = 0 и Х2==0, то любое движение по ои Xi или Х2 даст.уменьшение тока; однако, если двигаться наискось, в особенности в направлении А или В, амплитуда 72 увеличивается. При этом и Хз приходится изменять одновременно. На этой диаграмме легко понять физическое содержание частных резонансов.

Задав, например, какое-нибудь постоянное значение и изменяя мы пересечем местность в некотором направлении, причем всегда при некотором значении Ха достигнем более высокой точки, по обе стороны от которой начинается спуск. Это будет моментом частного резонанса. Легко также убедиться, что при очередной настройке на частные резонансы то при помощи Xi, то при помощи Xg мы с каждым разом приближаемся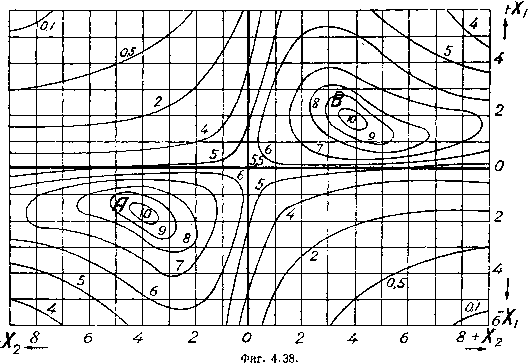

либо к вершине А, либо к вершине В, в зависимости от того, в каком месте находится точка, соответствующая исходному положению. Исключение составляет положение Xi = X2 = 0, когда поочередная перестройка Xj и Ха на максимум тока будет постоянно возвращать нас в исходное положение.

По мере уменьшения разности Xg - R1R2 обе вершины Л и В сближаются и при Хз = R1R2 сливаются в одну, расположенную в центре.

§ 14. Сводка результатов, полученных в предыдущих параграфаХч

Значение полученных выше математических результатов станет яснее, если проследить на примере изменение условий работы двухконтурной системы при изменении настройки контуров и связи между ними.

Начнем с того, что возьмем два контура, каждый из которых при отсутствии другого настроен на частоту со источника, включенного в первичный контур.

Настройка в резонанс означает, что

Xi = X2 = 0.

Будем сближать самоиндукцию этих контуров, вследствие чего между ними появится связь, определяемая взаимной индукцией М, которую мы

обозначаем

Амплитуда тока во вторичном контуре будет

(4.59)