Следовательно, здесь (как и в случае последовательного- включения) при возбуждении колебаний со стороны одного контура в системе

существуют две резонансные частоты, определяемые теми же формулами

(L-M)

{L-MI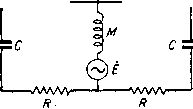

\ -к

2 ~ 1 -Н /с

где - собственная частота каждого контура, а к - коэфициент связи. Фиг. 4.32. Заметим еще, что при включении источ-

ника эдс в катушку свя5и М (фиг. 4.32) колебания получают тот же характер, что и при возбуждении конденсаторов при помощи эдс одинаковой фазы.

При таком возбугкдении существует только одна резонансная частота, определяемая равенством

§ 9. Математический анализ основных явлений.

Рассмотрим два контура без потерь, связанные посредством катушки М (фиг. И.ЗЗ). Этой схеме соответствует схема сопротивлений, показанная на фиг: 4.34.

(LfM)

Фиг. 4.33.

<5>

Фиг. 4.34.

Эдс Ё включена в первый контур. Тогда ток в цепи этой эдс будет

/ -А

где Z - входное сопротивление системы. На основании ур-ния (4.13) § 4 пишем

- z, + z, -

(4.22)

Из схем фиг. 4.33 и 4.34 видно, что Zi = /Lai -М)

i(L2 -М)

(oCi

(4.23)

Zg = j(aM.

Подставив эти значения в ур-ние (4.22), найдем

(4.24)

Это сопротивление равно нулю, если числитель ур-ния (4,24) равен нулю, что после открытия скобок запишем так

(LL,-Mn-- + 4e, = 0.

(4.25)

Обозначив

О), =

получим из ур-ния (4.25)

1-fc2

откуда

(4.26)

(4.27)

Если контуры настроены в резонанс, то = Шз = )о и ур-ние (4.27)

даст

(а) )2

1-fc

(4.28)

Ур-ние (4.28) приблизительно справедливо и в том случае, когда контуры обладают омическим сопротивлением если только

Это условие обычно имеет место в практически применяемых контурах. Вообще же для того, чтобы вычислить точное значение со и ш при наличии сопротивлений в контурах, надо, очевидно, подставить в ур-ние (4.22) значения

Z, = R + jUiLi-M) *

->CJ 1

Z2==R2 + i[<iE2-M)

7з = /соМ и решить его относительно со.

§ 10. Ток в первичном контуре.

Соответственно схеме фиг. 4 35 сделаем следующие обозначения

coLi

(4.29)

-4-)= X

C0L2 --

(LfM)

АЛЛЛЛг

Фиг. 4.35.

Тогда схеме фиг. 4.35 будет соответствовать схема сопротивлений фиг. 4.36.

Подставив в общее выражение для тока в первом контуре

/ = E(z,-z,)

ZjZy -- Z-Zq -j- ZZq

значения Zj, Zg и Zg из схемы фиг. 4.36, получим после преобразований следующее довольно сложное выражение

(4.30)

Для практики большое значение имеет такая настройка системы, ри которой входной ток становится чисто активным. Тогда мнимая часть ур-ния (4.30) должна обратиться в нуль.

Следовательно, в этом случае

ХзХз XXi i/?2

что можно переписать так

V 2 Y 2 Р !

(4.31)

Фиг. 4.36.

Так как стоящая в левой части величина х всегда положительна, то ур-ние (4.31) может быть удовлетворено только до тех пор, пока правая часть также положительна. Для этого должно быть

Хз Кг

кроме того мнимая часть обращается в нуль, если

Xi = X2 = 0.

(4.32)

Последнее соответствует одинаковой настройке контуров. Подставив в ур-ние (4.30) вместо Xg, его значение из ур-ния (4.31), получим после приведения подобных членов следующее простое выражение

/1 =

(4.33)

Ур-ние (4.33) показывает, что при удовлетворении условия (4.31) система представляет для эдс, включенной в первый контур, чисто активное сопротивление, равное

(4.34)