получим из ур-ний (4.17)

ri{\

Cl(i4-) 1+/С

(4.18) (4.19)

гдек = коэфициент связи. В данном случае Lj= L2 = L; поэтому к

§ 7. Кривые резонанса в случае двух одинаковых контуров, связанных между собой.

Мы видели, что в связанной системе, составленной из двух одинаковых контуров, может быть два типа колебаний. Первый тип характеризуется тем, что токи в катушке связи взаимно уничтожаются, а второй тем, что ток в катушке связи вдвое бошь-

{L-M}

/;=/; (L-M)

ше тока В контуре. Если эдс включена в первом контуре, то оба типа колебаний возможны и непосредственно неясно, какой именно из них возникнет и как будет протекать явление при разиичных нерезонансных частатах.

Чтобы выяснить этот вопрос, рассмотрим сначала случай, когда в каждом контуре существует эдс, одинаковая по амплитуде и по частоте. Сделаем фазы этих эдс одинаковыми. Тогда, как это показано на фиг. 4.25, получается только первый тип колебаний. Ток в катушке связи М равен нулю. Изменяя частоту эдс к, получим кривую резонанса для этого случая. Кривая будет соответствовать амплитудам тока,

а сам ток определится из ур-ния

Фиг 4.25.

(L-M)

-1ч --rL-M) -

(2)-АЛЛА/V--- R

2М 2М2

w(L-Л1)-

. (4.20)

Фиг. 4.26.

Изменим теперь фазу эдс во втором контуре на противоположную. Тогда получим колебания второго типа, как это показано на фиг. 4.26.

В силу полной одинаковости контуров тока в проводах А и В не будет, и каждый контур будет колебаться независимо один от другого.

Изменяя частоту эдс Е, получим кривую резонанса, соответствующую амплитуде тока как в первом, так и во втором контуре. Сами же токи определятся из уравнений:

а) для первого контура

б) для второго контура

/

ш (L -f М) -

R + /

.(L + M)-

(4.21)

Осуществим теперь оба типа колебаний одновременно. Для этого включим в каждый контур по две эдс соответственнЬ обоим случаям.

Тогда во втором контуре окажутся включенными одновременно две эдс, равные по амплитуде и периоду, но противоположные по фазе. Эти эдс взаимно уничтожаются. В первом же контуре обе эдс окажутся в одной и той же фазе, и амплитуда результирующей эдс будет равна их сумме.

Из этого следует, что включение эдс двойной амплитуды только в один первый контур совершенно равнозначно включению четырех эдс, при котором оба типа колебаний осуществляются одновременно. Поэтому в действительности при действии эдс 2Е только в первом контуре, ток в первом контуре будет равен

а во втором контуре

где 1[ и определяются ур-ниями (4.20) и (4.21).

Если пунктирные линии фиг. 4.27 и 4.28 изображают кривые резонанса для nepBdro и второго типа колебаний порознь, то сплошная кривая фиг. 4.27 . дает общую кривую резонанса в

/ - Л первом кон-цуре, а кривые фиг.

4.28 - во втором контуре. (Эдс предполагается включенной в первый контур.)

Кривая резонанса для ток в первом контуре получается как сумма, а во втором контуре - как разность пунктирных кривых с учетом, сдвига фазы. Поэтому ординаты этой кривой не являются простой суммой или разностью ординат пунктирных кривых.

Не вдаваясь в детали, отметим следующие важные обстоятельства, которые непосредственно очевидны.

а) Чем больше связь, тем дальше отстоят друг от друг-а резонансные частоты, а следовательно, и вершины пунктирных кривых. [См. ур-ния (4.18) и (4.19).] Поэтому тем резче выявлен двугорбый характер кривой резонанса.

б) Чем меньше декремент, тем острее пунктирные кривые, поэтому тем резче выявлен двугорбый характер кривой резонанса.

в) При достаточном уменьшении связи или увеличении декремента обе вершины пунктирных кривых могут настолько сблизиться или сделаться расплывчатыми, что у сплошной кривой исчезнет двугорбый характер и останется только одна вершина. Система потеряет свойство двухчастот-ности (или, как говорят, двуволнистости).

г) Если связь велика, а декремент при этом мал, то пунктирные кривые разойдутся далеко (фиг. 4.29) и практически сумма и разность их выразятся одной и той же сплошной линией, которая на чертеже не показана, так как она почти сольется с пунктиром. Из этого следует, что амплитуды токов в первом и втором контуре окажутся одинаковыми.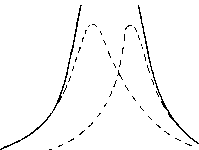

Фиг. 4.27.

Фиг. 4.28.

I 1 i \

Фиг. 4.29.

fL-M)

д) Наоборот, при большом декременте и малой связи сплошная кривая, выражающая разность пунктирных кривых с учетом сдвига фаз, пойдет значительно ниже кривой сум- j

мы, т. е, амплитуда тока во втором контуре будет значительно меньше, чем в первом, как это ясно из сравнения фиг. 4.27 и 4.28.

§ 8. Случай, когда эдс включена параллельно конденсатору.

Те же самые резонансные частоты связи получаются, если эдс включеа параллельно кон- /7

денсатору одного из контуров.

Чтобы перейти к этому случаю, рассмотрим две вспомогательные схемы.

а) Пусть I и II (фиг. 4.30) представляют собой два совершенно одинаковых контура, которые связаны общей катуш- , ? кой М. Приложим к их конден- Фиг. 4.30. саторам эдс Е таким образом,

чтобы эти эдс были направлены навстречу одна другой. Другими словами, сделаем так, чтобы потенциал в точке в любой момент был б,ы равен потенциалу в А, а потенциал в равен потенциалу в В.

В силу симметрии ток в контуре I одинаков с током в контуре II. В катушке М оба тока проходят в одном и том же направлении и образуют здесь двойной ток. При изменении частоты эдс резонанс наступит, когда

б) Повернем теперь фазу одной из эдс на 180°. Тогда опять-таки в силу симметрии токи в контурах останутся равными, причем по направлению один ток явится продолжением другого. Поэтому в катушке М оба

м п с =

fL-M)

С I

Фиг. 4.31.

тока взаимно уничтожатся, и эта катушка не играет никакой роли. Резонансная частота определится условием

СОо = -===. VC{L-M)

Соединив оба включения вместе, получим схему фиг. 4.31, из которой ясно, что в первом контуре амплитуда эдс останется прежней а во втором контуре не будет никакой эдс.