§ 9. Связь между экспоненциальными,

круговыми и гиперболическими функциями.

Мы видели, что

е = cos 6 -j- / sin 6.

Изменив знак у 6 на минус, получим

е -j = cos 6 - / sin 0.

Из этих двух уравнений легко получить

/sino =

(0.43) (0.44)

(0.45) (0.46)

Соотношения (0.45) и (0.46) представляют собой тождества, позволяющие выразить круговые функции через неперово число с мнимым показателем.

Полезно заметить! следующее графическое использование ур-ний (0.45) и (0.46). Выражение е- соответствует вектору А (фиг. 0.11), имеющему единичную длину и составляющему угол 6 с осью абсцисс. Выражение е соответствует такому же вектору В, составляющему угол-6 с осью абсцисс.

Геометрическая сумма этих векторов даст вектор С, лежащий вдоль оси абсцисс и соответствующий действительному числу 2cose.

Этот результат и дает ур-ние (0.46). Выполним геометрическое вычитание векторов А и В, получим вектор D, который определяется чисто мнимым числом /2 sin 6. Ур-ния (0.45) и (0.46) остаются справедливыми, будет ли дуга б действительным, мнимым или комплексным числом. Положим

б=/ср,

где р-действительное число. Тогда ур-ния (0.45) и (0,46) перепишутся так: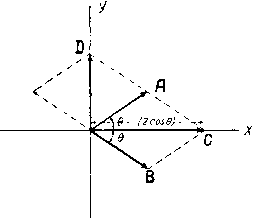

Фиг. 0.11.

-/sin (/с?)- 2

COS (/с?) =--

(0.47) (0.48)

Ур-ния (0.47) и (0.48) показывают, что .круговые функции от мнимого аргумента представляют собой уже не периодические функции. Они называются гиперболическими функциями и обозначаются так:

shcp (гиперболический синус).

- = ch9 (гиперболический косинус).

В графическом изображении гиперболический синус численно равен ординате СА (фиг. 0.12) точки А, взятой на равнобокой гиперболе с осями

00 - DE = \. Гиперболический косинус численно равен абсциссе ОС. Аргу ментом является удвоенная площадь 5 (заштрихованная на фиг. 0.12), заклю чающаяся между вет- qq вью гиперболы. ось1о абсцисс и линией, соединяющей начало координат с точкой А.

Гиперболические функции* аналогичны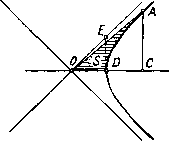

Фиг. 0;12.

UO и

Фиг. 0.13.

круговым, если за аргумент последних принять не дугу, стягивающую угол, а численно равную ей удвоенную площадь сектора, ограниченного этой дугой.

Функция ==th(cp) называется гиперболическим тангенсом, аобрат-/

. ch (ср)

пая функция

cth (ф) - гиперболическим котангенсом.

При изменении аргумента от нуля до бесконечности гиперболические функции кзменяются следующим образом: ch(cp) от единицы до бесконечности;

0.2 0.3 Фиг. 0.14.

1.10

01 02 аз

Фиг 0.15.

th(cp) от нуля до единицы; sh(cp) от нуля до бесконечности и cth(cp) от единицы до бесконечности.

Значения гиперболических функций для некоторого интервала аргумента даны на фиг. 0.13, 0.14 и 0.15.

Между гиперболическими функциями существуют соотношения, аналогичные тем, которые имеют место в круговых, и которые приведены 8 прилоаении I.

Таким образом между гиперболическими, круговыми, экспоненциальными и логарифмическими функциями существует прямое математическое родство.

При описании физических процессов переход от круговых функций к гиперболическим или (что одно и то же) переход от мкимых степеней к действительным соответствует переходу периодического процесса в апериодический.

Так например, пусть какая-нибудь физическая величина выражается функцией вида

£== е -

Если А>В, то изменение Е со временем носит апериодический экспоненциальный характер. Если же ВА, то Ё является периодической функцией времени.

Положив частоту мнимой <о == - /8, получим взамен периодических функций соответствующие экспоненциальные функции. Например,

Ате- и Ате-К

/7мплит1/лы пей синусffj[

шплитуды при косинясйх

§ 10 Понятие о линейчатых слектрах эдс и тока

Сложные формы кривых эдс или тока, встречающиеся в радиотехнике, могут быть гредставлены в, виде некоторой совокупности синусоидальных функций. Применение этого представления играет весьма важную роль в теории радиотехники и поэтому с ним следует хорошо освоиться.

Более простым случаем является такой, когда функция, которую хотят представить посредством синусоид и косинусоид, является периодической,

т. е. описываемое ею событие в точности и без конца повторяется через равные интервалы времени. К такой функции применяют разложение в ряд Фурье, после чего она представляется в виде суммы синусоид и косинусоид.

Эти суммы в здвнсимости от вида функции мо1*ут иметь конечное или бесконечное, число слагаемых. Но и в последнем случае 1сегда бывает возможным ограничиться конечным числом членов, дающим достаточное практическое приближение вследствие малости амплитуд остальных отброшенных членов ряда.

Совокупность всех членов ряда называется спектром данной функции, ,а каждый член ряда называется л ин и е й данного спектра. Такой спектр удобно изобразить графическим способом, показанным на фиг. 0.16. Для этого вдоль оси абсцисс наносится шкала частот. В точках, соответствующих частоте, имеющейся в данном спектре, восстанавливается перпендикуляр, длина которого в выбранном масштабе дает амплитуду эдс или тока (или другой физической величины), соответствующую данной частоте.

Перпендикуляры, направленные вверх, строятся для синусоиды или косинусоиды,- имеющей фазу, принятую за положительную.

Перпендикуляр!, направленные вниз, соответствуют колебаниям в противоположной, т. е. отрицательной фе.

Два таких графика, из которых один относится к синусоидам, а другой к косинусоидам, исчерпывающим образом характеризуют данную функцию.

Фиг. 0.16.