§ 3. Связь через сопротивление.

Если сопротивление R входит как в первый, так и во второй контур, как показано на фиг. 4.8, то при прохождении по контуру I тока l\, в контуре II возникает эдс x-,rrr

I-ОШР-,-пшг

ЛАЛ/VW

ЛЛЛЛЛАу-

Фиг. 4.8.

Так же при токе в контуре II появляется эдс в контуре I

£1 = / /?.

Такая связь называется непосредственной или кондуктив-ной связью через омическое сопротивление.

Слово кондуктивный обозначает, что обе цепи находятся одна с другой в электрическом контакте.

Кондуктивная связь может быть также осуществлена посредством включения вместо R некоторого комплексного сопротивления Z, как это, например, показано на фиг. 4.9.

Частным случаем кондуктивной связи является связь через самоиндукцию или емкость, как показано на фиг. 4.10 и 4.11.

ЛЛЛЛЛг

Фиг. 4.9.

2 А/

-ЛЛЛЛг

-ЛЛЛЛг

ЛЛЛЛЛг

ЛЛЛЛЛг

Фиг. 4.10.

Фиг.-4.11.

Если написать уравнения для двух последних случаев, то по своей форме они окажутся совершенно тождественными с случаем связи через взаимную индукцию или через взаимную емкость (соответственно).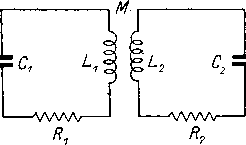

Фиг. 4.12.

2 -Г

-ЛЛЛЛЛЛ/-

ЛЛЛЛЛ/-

Фиг. 4.13.

Поэтому схему с индуктивной иди емкостной связью всегда можно эквивалентно заменить схемой с непосредственной связью.

Схема С индуктивной связью, показанная на фиг. 4.12, эквивалентно заменяется схемой с кондуктивной связью, показанной на фиг. 4.13. Также . схема фиг. 4 14 эквивалентно за-

-1 и Ь2 меняется схемой фиг. 4.15.

-RRHp-, <:,-птг

ЛЛЛЛЛг

Фиг. 4.14.

В случае схемы фиг. 4.13.

В случае схемы фиг. 4.15

§ 4. Связь в общей форме.

-ЛЛЛЛЛг

Сз=Мс

ЛЛЛЛЛЛ/-

ЛЛЛЛДЛг

Фи1. 4.15.

(4.11)

С,Мс

(4.12)

Как уже сказано, всякий вид связи может быть эквивалентно заменен кондуктивной связью. Каждая из связываемых цепей в свою очередь может рассматриваться как некоторое комплексное сопротивление. Поэтому две связанных цепи всегда могут быть приведены к эквивалентной схеме, показанной на фиг. 4.16.

Фиг. 4.16. Фиг. 4.17.

Эта схема в свою очередь при желании может быть эквивалентно заменена схемой фиг. 4.17, о чем будет сказано впоследствии.

Если в схеме фиг, 4.18 в первую цепь (Z) введена эдс Е, то токи

/j, /2 и /3 могут быть найдены по следующим формулам

2 Z,Z,-j-Z,Z,+Z,Z, EZ

(4.13) (4.14) (4.15)

Эти формулы дают решение задачи нахождения токов в самом общем виде. Рассматривая далее различные частные случаи, мы будем на них ссылаться.

Сделаем еще одно важное замечание. Посредством эквивалентной замены индуктивно 1ли емкостно связанных цепей цепями, связанными кон-дуктивно, мы достигаем того, что самые различные виды связи приводятся к одной и той же форме.

Изучая эту единственную форму связи, мы охватываем все возможные случаи. Это, однако, не значит, что на практике всегда возможно заменить индуктивную связь непосредственной даже при полном соблюдении эквивалентности. Дело в том, что установленная эквивалентность касается только переменного тока, но не касается постоянного тока или постоянных потенциалов. Рассматривая, например, анодную и сеточную цепи электронной лампы, связанные индуктивно, мы в праве заменить на схеме и при всех расчетах индуктивную связь непосредственной. Однако осуществить такую эквивалентную замену в реальной схеме нельзя, если ацодная и сеточная цепи находятся при разных начальных потенциалах. Могут быть и другие причины, не допускающие замены индуктивной связи кЪндуктивной или обратной. *

Это, оЛнако, ни в какой мере не лишает верности все расчеты и соображения, сделанные на основании эквивалентных схем.

Фиг. 4.18.

§ 5. Коэфициент обратной связи.

Если при токе /j в первом контуре образуется полный поток магнитных линий и если л-я доля этого потока пересекает катушку второго контура, то величину

М = 1

мы называем коэфициентом взаимной индукции. Очевидно, что

Так же, если во втором контуре под действием наведенной эдс возбуждается ток /2 и поток Фа, и если п-я доля этого потока пересекает катушку первого контура, то мы также пишем

М --

м

Очевидно, что произведение

п л., =

дает меру реакции или, иначе говоря, меру обратного воздействия, которое второй контур оказывает на первый посредством тока /3, возбужденного во второй катушке током первого контура.