ГЛАВА IV.

СВЯЗАННЫЕ СИСТЕМЫ.

ОБОЗНАЧЕНИЯ К ГЛ. IV.

С Е, е

/, i 1

к - L - М-Мс-Р -

К -t - X -

емкость эдс

основание неперовых логарифмов

сила тока

мнимое число Y-1 (оператор по-

ворота вектора на угол

коэфициент связи коэфициент самоиндукции коэфициент взаимной индукции коэфициент взаимной емкости мощность

активное (ваттное) положительное сопротивление вносимое сопротивление время

модуль реактивного сопротивления

комплексное выражение кажущегося сопротивления (Z = г 4- jx) поток силовых линий коэфициент затухания

Yj - коэфициент полезного действия

(кпд) z - период биений Q, (о, Д - круговая частота = - знак тождества

Амплитудные значения переменных величин обозначены большой буквой с индексом т, например, Е, 1, Р и т. д.

Постоянные и среднеквадратичные значения теми же буквами без индекса, например, Е, J, Р и т. д.

Мгновенные значения, выраженные в тригонометрической форме,обозначены малыми буквами, например, / = sin (<й/) и т. п.

Мгновенные значения, выраженные в комплексной форме, обозначены большой буквой с точкой наверху, например,

1=а + 1Ь:Е=Е

еЛ +й т.д.

§ ]. Магнитная связь.

Две электрические цепи называются связанными, если при прохождении переменного тока по одной цепи в другой цепи наводится эдс. Связь всегда имеет взаимный характер, т. е. если первая цепь способна возбудить

эдс во второй цепи, то и обратно- при прохождении переменного тока по второй цепи, в первой будет наводиться эдс.

На практике связь между цепями может быть осуществлена различными способами. Рассмотрим индуктивную связь.

Цепь I фиг. 4.1 связана с цепью II взаимной индукцией, т. е. при прохождении тока по катушке Л, принадлежащей цепи I часть силовых линий пересекает катушку Б, принадлежащую к цепи II.

Фиг. 4.1.

Вследствие этого в цепи II наводится эдс

где Л - ток в первой цепи, а М - коэфициент взаимной индукции.

Так же при прохождении тока по второй цепи в первой наводится эдс

= - /шМ/а.

Положим, что в одной из цепей (например, в цепи I) действует источник переменной эдс Е (фиг. 4.2). Пусть эта цепь представляет собой

контур с емкостью Cj, самоиндукцией Lj и сопротивлением R, равным образом, как и связанная с ней вторая цепь с параметрами Cg, Lg и R. Коэфициент взаимной индукции обозначим М.

Если бы между контурами не было взаимной связи, то ток в первом контуре определился бы из г равенства о

причем

(4.1) о

(4.2)

I 12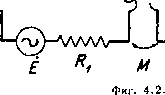

ЛЛЛАЛг

Однако, так как между катушками существует взаимная связь и во втором контуре (под действием первого) существует ток /а, то кроме эдс Е в первом контуре появляется еще эдс

El = - /(оМ/а, вследствие чего взамен ур-ния (4.1) надо писать

1 £ - /мМ/г

(4.3)

Откуда легко получить

E = {Ri-hMi + /i-f /соМ/а. (4.4)

Для второй цепи уравнение будет иметь аналогичный вид, но так как в этой цепи единственнымИСТОЧНИКОМ эдс является взаимная индукция, то

взамен Ё пишем нуль

О = ( /?а + /coL, + ) /а + / Л!А. (4.5)

Два ур-ния (4.4) и (4.5) дают возможность найти и /а, если Ё и параметры цепей заданы.

§ 2. Емкостная связь.

На фиг. 4.3 показаны две цепи, связанные через взаимную емкость. Такая связь практически осуществляется, если электрическое поле конденсатора Cl проникает в конденсатор Cg.

На фиг. 4.3 показаны, например, два конденсатора Cj и Cg, емкостная связь между которыми обусловлена тем, что часть поля одного конден-

лл/w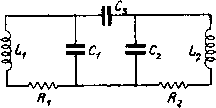

Фиг. 4.3.

Фиг. 4.4-

сатора занимает тот же участок пространства, что и часть поля другого конденсатора.

На фиг. 4.4 показан способ осуществления емкостной связи через параллельный конденсатор Сд.

На фиг. 4.5 показаца схема емкостной связи посредством включения последовательного конденсатора Mq, общего для обоих контуров.

Всякая схема с взаимной емкостью может быть эквивалентно приведена к схеме фиг. 4.5. Здесь емкость Мс является общим звеном, связывающим две цепи - I и П.

Если в первой цепи идет ток l\, то во второй цепи появляется эдс, равная по величине падению напряжения на конденсаторе Мс Поэтому уравнения для этих цепей напищутся следующим образом

-ЛЛЛАЛг

Фиг. 4.5.

Если обозначить

то эти уравнения можно переписать так

(4.6) (4.7)

(4.3)

(4.9) (4.1Р>

Здесь Cj и Cg представляют собой емкости первого и второго контура взятых в отдельности (фиг. 4.6).

Величина Мс называется коэфициентом взациной емкоср.

РПВНО

Фиг. 4.6.

АЛЛЛл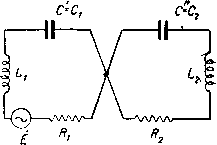

Фиг. 4.7.

Ясно, ЧТО связь между контурами тем сильнее, чем больше относительная величина множителя . Поэтому связь растет с уменьшением Мс

и падает с увеличением Мс.

Если Мс = оо, то проводимость /оМс = оо, а это равносильно короткому замыканию.

В этом случае контуры касаются один другого в одной точке (фиг. 4.7) и никакой связи между ними нет.