Фиг. 3.44.

Было бы, одйако, совершенно неправильно думать, что этим путем колебательные системы создают свои собственные частоты. В действительности они только выделяют из спектра действующей эдс некоторые полосы частот, которые соответствуют свободным колебаниям и которые обязательно должны уже содержаться в действующем на систему спектре.

§ 22. Устанавливающийся режим при сигнгах.

В радиотехнике телеграфные сигналы подаются чаще всего посылкой коротких и длинных групп незатухающих колебаний.

Так например, на фиг. 3.44 графически изображена кривая тока (или напряжения , соответствующая букве д (тире две точки).

В приемном устройстве в контуре, настроенном на частоту колебаний, индуктируется эдс, характеризуемая такой же кривой (фиг. 3.44). Далее, под действием эдс в контуре возникает ток, амплитуда кото- рого нарастает и спадает согласно тем законам, которые были выведены.

Таким образом общий характер кривой тока получается таким, как это показано на фиг. 3.45.

Амплитуда тока нарастает и постепенно достигает

некоторого значения, после которого дальнейший рост практически не имеет значения.

Когда эдс прекратила свое действие, амплитуда тока начинает спадать. И нарастание и спад идут, разумеется, тем медленнее, чем меньше затухание контура.

Контур с очень малым затуханием может совершенно размыть сигнал и слить отдельные его чсти в одно целое. Сигнал станет неразборчивым и это может затруднить, или даже сделать невозможным, его прием. Такое явление будет наблюдаться тем резче, чем меньшее число периодов колебаний укладывается на

[ протяжений одной по-

сылки (группу колебаний) или на протяжении интервала ме}&ду посылками.

Чем медленнее идет передача и чем выше частота колебаний, тем менее заметен будет этот эффект размывания сигнала при том же декременте затухания контура.

С другой стороны, малый декремент контура необходим для того, чтобы можно было отфильтровать, т. е. отделить данный сигнал, подающийся на какой-то полосе частот от со до со, от всяких других чужих сигналов, подающихся на частотах со, СО3.., и т. д.

Таким образом здесь вступают в противоречие два требования: требование быстродействия, т. е. ускорения ритма посылок (и поэтому сокращения длины каждой посылки), противоречит требованию применения остро настроенных цепей, необходимых для выделения данного сигнала. Разрешение этого противоречия заключается в правильном сочетании обоих требований.

Для того 4to6bi это сделать, мы должны несколько глубже проанализировать физическое содержание этого противоречия. Здесь мы подходим к одному из основных явлений радиотехники, с которым не раз еще встретимся. Правильное понимание и рациональное теоретическое представление об этом явлении крайне важно, и читатель должен особенно внимательно

Фиг. 3-45.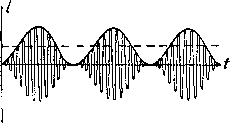

Фиг. 3.46.

отнестись к следующим разъясйениям, дающим простой и универсальный ключ ко многим сложным явлениям.

Если данный контур, являющийся линейной системой, не может воспроизвести без искажения данный сигнал, это обязательно и соверщенно непреложно означает, что спектр данного сигнала после прохождения через контур существенно искажен.

Совершенно нет надобности детально исследовать, как нарастают и спадают колебания в контуре для того, чтобы сказать, будет\ искажен сигнал

или нет. Для этого достаточно знать: а) каков спектр сигнала в своей существенной части и б) какова полоса пропускания частот данным контуром (или другим фильтром).

Обе эти величины обычно легко н при помощи простых приемов могут быть определены. Нарастание же и спад тока или * напряжения в контуре могут иметь бесчисленное количество вариантов и доступны исследоэанию только в более простых случаях.

Что касается спектра телеграфного сигнала, то он состоит из отдель* НЫХ посылок, а каждая посылка состоит из отрезка синусоиды. Для того чтобы пропустить совершенно без искажения весь сигнал, необходимо равномерно пропустить спектр кривой, состоящий из самого короткого отрезка сик[усоиды. Однако это является недостижимым идеалом, так как этОт спектр сплошной и ширина его простирается от ш = 0 до ш==оо. Поэтому данный спектр без всякого искажения пропустить принципиально невозможно. Следует выбрать такую меру искания, при которой сигнал оставался бы доброкачественным, а фильтр не пропускал бы вместе с тем слишком широкую полосу частот, так как это увеличило бы количество помех.

Рассмотрим в качестве примера телеграфный сигнал, подаваемый азбукой Морзе. Положим, что сигнал состоит только из точки и что в секунду подается 150 точек. Вследствие искажения каждый сигнал вообще будет искажен в том смысле, что и начало и конец его,

как только что было показано, будут не- I i i-(j

сколько размыты. (}, CJ СО.

Будем считать пределом допустимого искажения такое, при котором ряд последовательных точек даст кривую, показанную на

фиг. 3.46, и посмотрим, какими свойствами должен обладать фильтр, чтобы пропустить подобную кривую без существенных искажений.

Огибающую не фиг. 3.46 предположим для простоты синусоидальной. Тогда вписанная в нее высокочастотная кривая может рассматриваться как результат биения трех частот /о - частоты передатчика (в герцах) и (/о-j-n) и {fo - n), где л-число точек в секунду, т. е. в данном случае 150.

Спектр этой кривой показан на фиг. 3.47. Величина (Оо = 2тс/о; A = 2i:n.

Чтобы фильтр пропускал без искажения рассматриваемые колебания, надо, чтобы в пределах спектра полосы не было заметной разницы в прохождении различных частот. За меру допустимого отклонения тока от его максимального значения примем величину 0,7, т. е. будем считать, что полоса пропускания контура ограничена частотами, при которых квадрат амплитуды тока вдвое меньше квадрата амплитуды при резонансе (фиг. 3.48).

Эта мерка, разумеется, соверщенно условна, но практически она пригодна для большинства форм сигналов. Удобство ее заключается в следую-

Фиг. 3.47.

щем. Как мы видели, квадрат силы тока уменьшается вдвое при отходе от резонанса на частоту А, численно равную коэфициенту затухания контура (§ 19). Поэтому для того, чтобы контур пропустил полосу частот от w - А до со А и амплитуды при этих крайних частотах были бы ослаблены 0,7 раз надо сделать коэфициент затухания 8 равным половине ширины полосы. Таким образом должно быть

Д = 2тсл = 8.

В нашем случае при п = 150 8 = 2тсл1000.

Если частота, на котброй ведется передача, будет, например, 10 гу. (что соответствует волне 3000 м), то логарифмический декремент контура должен быть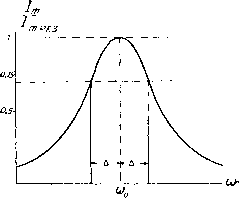

Устроить контур СО СТОЛЬ малым декрементом возможно, хотя и довольно трудно.

Если бы передача шла на волне 300 м (/ = 10 гц), требуемый декремент получился бы равным

== = 1 = 0,001.

Такой декремент практически не может быть получен в одиночном контуре и поэтому для надлежащей фильтрации потребовалось бы прибегнуть к нескольким контурам или к особым устройствам с электронными лампами.

Наоборот, если бы была применена волна 30 000 л, то потребовался бы декремент 0,1, т. е. контур с относительно сильным затуханием.

Рассматривая передачу телеграфного сигнала, мы от формы кривой сигнала перешли к спектру. Чаще, однако, бывает, что с самого начала задан именно спектр сигнала или, по крайней мере, ширина этого спектра. Например, кривые микрофонного тока при разговоре мфгут быть бесконечно разнообразны, но спектр их содержит частоты от 30 до 10000 гц, а для коммерческой телефонии из этого диапазона существенным оказывается только интервал частот dT 300 до 3000 гц.

Было бы невозможно охватить аналитически все комбинации нарастания и спада кривых телефонного тока в различных контурах с целью выяснения искажений вследствие устанавливающегося режима. Метод спектра дает на это непосредственный и совершенно исчерпывающий ответ: если данная цепь (например, контур) пропускает без значительного ослабления все частоты спектра и если изменение фазовых сдвигов не играет роли, то существенных искажений не будет.

Фазовые сдвиги играют роль в редких случаях, и тогда надо обследовать еще и эту сторону вопроса.

Что же касается несущественных изменений, то они будут обязательно во всех случаях, когда применяется колебательная система, хотя не всегда их можно практически обнаружить.

Эти искажения будут обусловлены теми частями спектра, которые мы ради простоты не принимаем в расчет, представляя спектр сигнала ограниченным полосой частот, в то время, как он всегда простирается во всей области возможных частот.