Коэфициент затухания S приблизительно равен разности между часто-той резонанса и той частотой, при которой ток в контуре уменьшается в У 2 раз.

Практически разность частот измерять не так удобно, как отношение частоты при резонансе к другой какой-нибудь частоте.

Помножив обе части ур-ния (3.90) на , получим

2пА =8 2=0 = 2тгА.

о) со COq

Таким образом, если по оси абсцисс кривой резонанса откладывать не величину А, а отношение , т. е. относительную расстройку цепи, а по

ОСИ Ординат-jp--, то ординаты уменьшатся вдвое в тот момент, когда

т рез

численно будет равно логарифмическому декременту.

Сказанное здесь для простоты отнесено к случаю последовательного сопротивления.

В случае параллельного сопротивления как характер рассуждений, так и окончательный результат ничем яе отличаются.

§ 20. Устанавливающийся процесс в контуре под действием внешней эдс.

Рассмотрим теперь процесс развития колебаний в контуре под действием внешней незатухающей эдс, включенный в некоторый момент (который обозначим как / = 0>, и далее длящийся неопределенно долгое время.

Уравнение этой эдс пусть будет

е = 0 при f<0

е = Ет cos {Ы) при t > О

Для того чтобы написать уравнения для тока в контуре под действием этой эдс можно воспользоваться уже полученными ранее результатами при помощи следующего примера.

Мы полагаем, что эдс, действующая на кбнтур, не равна нулю при f<0 и выражается тем же уравнением, как и при />0.

Другими словами, мы полагаем, что эта эдс существует вечно и выражается уравнением

е = Ет cos (Ы) при t от - оо до-j-оо. (3.91)

Для того же, чтобы восстановить действительное положение вещей, мы полагаем, что кроме этой эдс существует еще другая, которая выражается тем же законом, но с обратным знаком, и длится только до момента / = 0

Эта вторая эдс выражается, следовательно, так:

2 = 0 при/>0 )

е = -Ет cos (соО при / < О 1

Сумма эдс 1 и 2 дает ту самую эдс, которая существует в действительности

е-\-ее. (3.93)

Ток в контуре при таком представлении будет состоять из двух слагающих. Это будет, во-первых, ток г, который соответствует эдс е. Он

определится по формуле для установившегося режима, так как эдс действует сколь-угодно долгое время

/ - н - Z

где Z - комплексное сопротивление контура для данного включения эдс. Этот ток будет существовать все время от i - - co до f ---оо.

Вторым слагающим будет ток, образованный эдс 2, который к моменту / = 0 определится такой же формулой установившегося режима и будет равен

= (3.95)

где Z - то же самое сопротивление.

Полный ток до момента = 0 будет

/==/1-1-/2 = 0. (3.96)

После момента f = 0 ток /1 будет продолжаться, вместо же тока /д в

контуре появится новый ток /3, соответствующий затухающим колебаниям, которые возникают в контуре вследствие прекращения действия эдс е.

Начальными условиями этих колебаний являются те заряды и токи, которые были созданы эдс к моменту ее исчезновения, т. е. к моменту t - 0. Эти условия всегда легко вычислить из ур-ния (3.95).

В простейшем случае, который мы здесь рассмотрим, а именно, когда эдс е присоединена к обкладкам конденсатора С и контур настроен на частоту эдс, в этом вычислении даже нет надобности, так как очевидно, что к моменту = 0 эдс

егЕт ]

а эдс I (3.97)

2 ~ Ещ J

Следовательно, после t = 0 мы будем иметь, во-первых, ток zl, который в случае малого затухания контура при настройке контура в резонанс будет

i,=Emy sinH) (3.98)

и, во-вторых, ток /3, который будет представлять собой затухающее колебание, соответствующее начальному заряду конденсатора, равному - Ет.

Если затухание невелико, то на основании полученных ранее результатов этот ток будет равен,

z3== -£тЛ -e-ssin(<oO, (3.99)

где <о - собственная частота контура, совпадающая с частотой эдс, а 8 - коэфициент затухания

Таким образом в рассматриваемом простейшем случае, когда действующая частота совпадает с собственной частотой контура

i i,-f- i, = Em - e-O sin 1шО. (3.100)

На фиг. 3.<2 показаны кривые для случая, когда действующая частота совпадает с собственной частотой контура.

На фиг. 3.43 показан случай, когда действующая частота не совпадает с собственной частотой контура.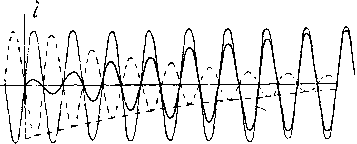

Фиг. 3.42. Толстой линией обозначен суммарный (действительный) ток, пунктиром-затухающие свободные колебания, тонкой линией- вынужденные колебания.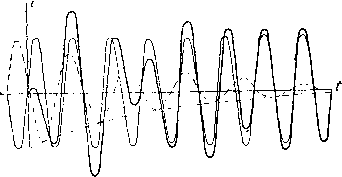

Фиг. 3.43. Толстой линией обозначен суммарный (действительный) ток, пунктиром-затухающие свободные колебания, тонкой линией- вынужденные колебания.

Тонкая линия соответствует току i. Пунктирная линия соответствует току затухающего колебания iV Жирная линия дает сумму обоих токов, т. е. действительный ток в контуре.

§ 21. Свободные и вынужденные колебания.

В связи с указанным представлением в контуре обычно рассматривают два тока: вынужденный , т. е. возникший под действием эдс (и имеющий период этой вынуждающей эдс ) и свободный , т. е. ток, который соответствует эдс е.

Свободный ток, следовательно, имеет затухающий характер и имеет частоту, свойственную данному контуру.

Полный ток есть сумма ,свободного и вынужденного .

Свободный ток, или говоря иначе, колебания с периодом, свойственным самой колебательной системе, возникают при всякой перемене режима действующей эдс. Сюда относится уменьшение или увеличение амплитуды, изменение периода или фазы эдс, появление новых периодических эдс или отдельных толчков.

На все это колебательная система обязательно отзовется в форме появления в ней колебаний свойственного ей периода. Эти колебания далее затухают со свойственным системе коэфициентом затухания.

Явление это играет иногда большую практическую роль, так как контуры и вообще системы, способные колебаться, как бы навязывают свои свободные колебания, создавая этим помехи.