§ 17. Токи и напряжения при свободн]ых колебаниях контура с потерями.

Выражения для токов и напряжений были уже написаны в общем виде а § 15 [ур-ние (3.79)] для контура без потерь.

Чтобы перейти к контуру с потерями, надо в этих формулах подставить взамен L значение взамен С значение С и взамен < > значение

(З.В5)

причем в ур-нии (3.85) L и С представляют собой емкость и самоиндукцию icoHTypa с потерями, а о и 3 Определяются формулами § 16.

Характеристика волнового сопротивления контура с потерями будет

Для практически применяемых контуров, ввиду малости R по срав* яениЮ/С (oL и g по сравнению с <оСу обычно пренебрегают мнимыми составляющими и пишт / 27

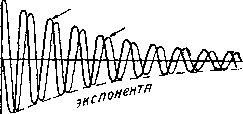Фиг. 3.40.

С3.86)

Поэтому для случая, когда разряд начался с момента / = 0, когда ток s контуре был равен Imx, а напряжение на конденсаторе было Е, ур-ния (3.79) § 15 перепишутся следующим образом

Ha фиг. 3.39 показаны кривые колебаний для случая, когда первона- чально существовал только заряд на конденсаторе.

На фиг. 3.40 показаны кривые для случая, когда первоначально суще-? <твовал только ток jb самоиндукции.

§ 18. Различные характеристики контура с потерями.

Из характеристик контура выше уже упоминались характеристическое сопротивление j/ и коэфициент затухания (8). Укажем еще некоторые характеристики.

Промежуток времени Т между моментами, когда ток (или напряжение) в контуре, проходя через нулевое значение, одинаков во все время колебаний и равен

~ со

называется собственным периодом колебательного контура. Если 8<(о, то приближенно можно написать

Если емкость измерять в сантиметрах (т. е. в CGSe системе) а самоиндукцию также измерять в сантиметрах (т. е. в CGSp. системе), то* получим

где с-скорость света.

Так как произведение Тс дает длину волны, то

Тс X = 27Г i/LcmCcm} (3.87)

Эта волна называется собственной волной контура , Ф-ла (3.87) носит название формулы Томсона .

Следующей важной характеристикой контура является так называемый логарифмический декремент затухания.

Если в некоторый момент времени ток имел значение /j, а спустя один

период получил значение i, то отношение остается постоянным и не

зависит от /. Действительно,

e-4in(<oO

ткуда

87 = In il - In /2 =

Эта величина называется логарифмическим декрементом затухания контура и Н случае 8<С > может быть выражена равенством

Если g == оо, т. е. утечки на конденсаторе нет, то

= 2-2Т-> =

Чем меньше логарифмический декремент, тем за большее число периодов амплитуда колебаний уменьшится в некоторое заданное число раз.

Величина, обратная декременту, показывает, сколько периодов колебаний пройдет до момента, когда амплитуда уменьшится в е раз. Действительно,. экспоненциальный множитель, определяющий затухание, равен е--Его можно написать и так:

е- е-Ч+).

Применяя выражение , мы измеряем время, измеренное не секундами, а числом периодов. Если амплитуда уменьшилась в е раз, то

= 1,

а следовательно, число периодов равно

L L г ~

Легко показать, что декремент затухания пропорционален отношению мощности к вольтамперам.

§ 19. Определение декремента затухания посредством кривых резонанса.

Коэфициент затухания и декремент могут быть определены из кривой резонанса контура.

Уравнение для такой кривой было дано в § 2, ф-ла (3.4) в следующем виде

/га рез 1 /

Перепишем его так

от рез

i?2 1

(3.88)

где <0q - собственная частота контура, равная-,--

Если затухание не слишком велико, то значительные изменения отношения

/ 2 /га рез

произойдут при относительно небольшом отступлении действующей на контур частоты <о от резонансной частоты (Oq. ?

Поэтому положим, что 1т

где А переменная величина, малая по сравнению с (а.

Тогда, имея в виду, что в ур-нии -

(3.88)

трЕЗ

.t№ = 2Д. (3.89)

напишем

у 2 от

Т~2 /га рез

1 + А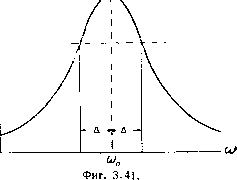

Отношение-у-х-станет равным половине (фиг. 3.41), если

от рез

А = 8.

Это дает возможность непосредственно измерить значение §.

(3.90) 137