Полагаем решение его в виде

/=ЛеР (3.57)

Подставив в ур-ние (3.56) ур-ние (3.57), найдем

LpAtPi + RAePt = О, (3.58)

Lp + i? = 0. (3.59)

Отсюда

(3.60)

Следовательно,

г = Ле~Т (3.61)

Начальное условие заключается в том, что при / - О, / = поэтому

г = / е-Т. (3.62)

Ур-ние (3.62) показывает, что с момента предаставления системы дамой, себе ток уменьшается по экспоненциальному закону и притом тем

быстрее, чем больше отношение -j-.

Для того чтобы рассмотреть случай, когда постоянная эдс внезапно включена в цепь в момент времени t, заменим эту эдс

е==Ет при f>0, = 0 при /<0

двумя эдс, а именно:

ех==Ет при t от - оо до -оо,

- Ет при /<0.

Первая эдс, действуя бесконечное время, создаст в цепи к моменту 1 = 0 ток

il = /т.

Вторая эдс к этому же моменту создаст ток

2 ~ т

Оба тока взаимно уничтожаются.

С момента = 0 вторая эдс исчезнет. Оставшийся от нее ток уменьшается по найденному закону, т. е.

2 ~ Im

Ток первой эдс остается неизменным.

Поэтому общий ток (существующий в цепи) будет

(3.63)

Это уравнение показывает, что после включения постоянной дс ток в цепи нарастает, постепенно приближаясь к предельному значению, определяемому для данной цепи законом Ома

Скорость нарастания тока зависит от показателя - -ji- Промежуток

времени называют постоянйой времени данной цепи. Чем постоянная времени больше, тем медленнее идет нарастание тока. Режим называется установившимся, когда ток достигает такого значения, что дальнейшее его возрастание не имеет практического значения.

б) Разряд емкости через сопротивление.

Пусть в цепь,- состоящую из емкости С и сопротивления г (фиг. 3.34), включена эдс Ет, действующая неограниченное время до момента f = 0> когда источник эдс внезапно замыкается накоротко. Тогда конденсатор начинает разряжаться через сопротивдение г, и в последнем появляется ток /.

Диференциальное уравнение для этого случая будет

так что

откуда

(3.64)

(3.65) (3.66)

также

i=-?e

(3.67)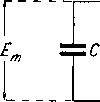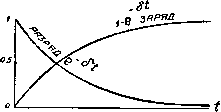

ФиР. 3.34.

Фиг. 3.35.

Ур-ния (3.66) и (3.67) показывают, что разряд будет происходить по тому же закону, что и в случае самоиндукции, с той только разницей, что постоянная времени теперь выражается величиной

х = Сг.

Совершенно так же, как это было показаноЗ[выше, можно получить выражение для случая, когда эдс Ет включена в момент времени f=0. Получим

(3.68)

е = Е,

1 -е

(3.69)

Характер кривых, выражающих зависимость е- и (1 - е-0, показан на фиг. 3.35.

S 15. Свободные колебания в контуре без потерь.

Рассмотрим теперь раЗряд в контуре, состоящем из емкости и самоиндукции (фиг. 3.36), Для математического анализа явления надо написать дйференциальные урашения, выражающие условия равенства эдс и тока.

Очевидно, что в каждый момент напря-

жие на конденсаторе Ёс уравновешивается шаяряжением на самоиндукции. Поэтому в кон- /- ( Tvype без потерь будем иметь

(3.70)

О О

Напряжение на конденсаторе зависит от емкости С и количества/электричества q, перенесенного током /,

Ec~q=-4r

idt.

Поэтому ур-нне (3.70) можно написать так

z. + j = 0;

отсюда

(3.71)

Ур-ние (3.71) показывает, что ток представляет собой такую функцию времени, вторая производная которой равна самой функции, разделенной т LC и взятой с обратным знаком.

Этому условию удовлетворяет экспоненциальная функция с мнимым

показателем Ае . Поэтому в ур-нии (3.71) взамен символа можно написать символ /о). Получим

откуда

= >n.

(3.72)

Решение ур-ния (3.71) 6yAef, следотельно,

Кроме того,- имея в виду, что

1 = Ё]фС

(где Я - напряжение на конденсаторе), можно написать второе уравнеш!е

Отсюда

(3.73)