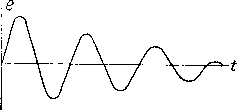Фиг. 3.27.

Учесть эти неточности чисто теоретическим путем весьма трудно в каждом частном случае; поэтому в радиотехнике наряду с расчетом необходимо применение измерений и различных расчетных таблиц, полученных на основании эксперимента.

§ 13. Предварительные замечания

об устанавливающихся процессах в контуре.

До сих пор мы рассматривали явления в контуре в установившемся режиме и поэтому могли пользоваться символическим методом. Мы могли бы использовать тот же метод для исследования устанавливающегося режима посредством следующего приема.

Положим, что в контуре действует некоторая эдс, например, выражающаяся во времени кривой фиг. 3.27, и мы хотим узнать, как будет изменяться

во времени ток в контуре, состоящем, например, из С, L и Й.

Представим нашу кривую в виде спектра эдс, т. е, в виде суммы большого или бесконечного числа эдс различных амплитуд, частот и фаз.

Эти эдс, составляющие спектр, будут длиться от/ = - оо до / = -}-оо, и поэтому мы застаем в момент времени t - 0 и во все последующие моменты уже установившийся режим для всех эдс. Каждой эдс будет соответствовать некоторый ток, который легко определить, зная устройство контура. Все токи в совокупности дадут некоторый спектр тока. Этому спектру будет соответствовать некоторая кривая тока, которая дает ответ на поставленный вопрос.

Этот путь является универсальным и пригоден для любого случая. Мы им, однако, не можем здесь воспользоваться вследствие его сложности и необходимости некоторого расширения математических сведений читателя.

Поэтому мы остановимся только на некоторых наиболее интересных частных случаях устанавливающегося режима и раньше, чем приступить к математическому анализу, рассмотрим явления качественно со стороны их физического содержания. Здесь нам большую помощь может оказать физическая аналогия из области механических явлений, которой МЫи воспользуемся.

Представим себе маятник, состоящий из груза М, подвешенного на нити, закрепленной в точке К (фиг. 3.28), и способного совершать колебания. Положим, что под действием какой-то причины маятник колеблется, и мы застаем его в некоторый момент в крайнем левом положении (фиг. 3.29).

В этот момент груз М поднят по отношению к своему среднему положению и обладает некоторым запасом энергии. Сила тяжести, стремясь опустить груз, сообщает ему ускорение, вследствие чего он начинает двигаться вниз и вправо, постепенно теряя свой запас потенциальной энергии и приобретая скорость, т. е. запас кинетической энергии. Когда через V4 периода колебания нить маятника примет отвесное положение, вся его потенциальная энергия окажется израсходованной, но зато около этого момента груз будет иметь максимальную скорость, т. е. максимальный запас кинетической энергии.

Фиг. 3.28.

Фиг. 3.29.

Кинетическая энергия в следующие V4 периода вновь переходит в па-тенциальную, и груз, двигаясь вправо, постепенно поднимается, пока не Достигнет крайнего правого положения. Теперь опять вся энергия маятника получила потенциальную форму, и процесс колебаний начнется вновь уже в противоположном направлении.

С каждым размахом амплитуда колебаний становится все меньще и меньше, потому что часть энергии затрачивается на преодоление различных трений.

Изображенная графически кривая колебаний получает вид затухающей синусоиды (фиг. 3.30). Затухание идет тем медленнее, чем больше запас энергии маятника по сравнению с потерями мощности на трение.

Если относить затухание на каждый перцод, то можно сформулировать это и иначе: относительное уменьшение амплитуды в течение периода тем меньше, чем больше реактивная мощность маятника (запас энергии, поделенной на длину периода) по сравнению с активной мощностью (расходуемой на трение).

Совершенно такая же картина должна получиться и в контуре.

Положим, что мы застаем контур в том момент, когда заряд на конденсаторе достиг максимума, а ток в самоиндукции равен нулю. Пусть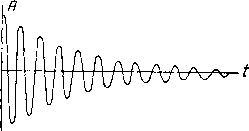

Фиг. 3.30.

Фиг. 3.31.

С ЭТОГО момента всякая внешняя эдс отсутствует. Начнется разряд конденсатора и через некоторое время конденсатор разрядится. Однако за время этого разряда при малой величине сопротивления энергия не могла перейти в тепло. Это значит что она продолжает существовать в контуре в другой форме, а именно - в форме магнитного поля. Это соответствует тому факту, что напряжение на конденсаторе сдвинуто по фазе по отношению к току на угол 90°.

Следовательно, так же, как в маятнике, потенциальная энергия электрического заряда перешла в кинетическую энергию магнитного поля.

Далее магнитное поле, исчезая, поддерживает ток того же направления, которое он имел в момент своего максимума. Этот ток, заряжает конденсатор вновь, но заряд имеем знак, противоположный предыдущему.

После этого начинается обратный процесс, заканчивающийся вновь зарядом конденсатора с той же полярностью, как и в самый первый момент.

Этот процесс носит название электрических колебаний. Колебания постепенно затухают так же, как и колебания маятника.

Относительное уменьшение амплитуды за один период тем больше, чем больше энергия, расходуемая в сопротивлении за один период по отношению к запасу энергии контура. Иначе говоря, чем больше активная мощность по сравнению с вольтамперами.

Если маятник поместить в очень вязкую среду или в контуре очень увеличить сопротивление, то колебания прекратятся, и явление примет апериодический характер, которому соответствует кривая фиг. 3.31.

Апериодический разряд будет во всяком случае иметь место в том случае, если угол сдвига фазы между током и напряжением в контуре будет близок к нулю, так как тогда одновременно с исчезновением напряжения исчезнет и ток.

Наоборот, даже при очень большом расходе энергии, если угол Сдвига фазы близок к 90°, разряд может весьма быстро затухать, но останется колебательным.

Рассмотрим теперь обратный процесс, а именно процесс раскачивания под действием внешней периодической силы. Прилагая к маятнику толчки через равные промежутки времени, мы вызовем процесс его раскачивания. Однако, если эти толчки по своему периоду не будет совпадать с периодом маятника,- его раскачивание не достигнет большой амплитуды. Некоторые толчки будут попадать в такт с колебаниями. Тогда маятник будет получать энергию, отбирая ее от толкающего механизма. Другие толчки

попадут не в такт и замедлят раскачивание. Маятник в эти моменты будет, наоборот, отдавать свою энергию толкающему механизму.

Если же период толчков в точности совпадает с собственными периодами маятника, раскачивание будет итти непрерывно и закончится тогда, когда вся мощность толкающего механизма будет расходоваться на различные трения, будет иметь место и в случае контура, находя-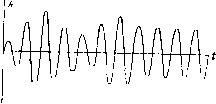

Фиг. 3.32.

Аналогичное явление щегося под Действием эдс.

Максимальная возможная амплитуда в установившемся режиме в контуре будет соответствовать случаю, когда собственный период контура совпадет с периодом вынуждающей эдс. Мы уже знаем, что в контуре с последовательным сопротивлением и последовательной эдс этому соответствует частота

Из этого следует, что и при свободных затухающих колебаниях частота должна быть близкой к этой величине (хотя несколько и может отличаться, так как процесс носит затухающий характер).

При Несовпадении частоты вынуждающей эдс с собственной частотой контура процесс будет иметь сначала характер чередующегося усиления и ослабления колебаний (как на фиг. 3.32), а затем уже установится на некотором уровне амплитуды.

§ 14. Разряд самоиндукции и емкости через сопротивление.

£

Фиг. 3.33.

Рассмотрим еще два случая устанавливающегося режима в более простых цепях, образованных из контура, в котором Ь= О или С = ос.

а) Разряд самоиндукции через сопрот ивление.

Пусть в цепи, составленной из последовательно соединенных сопротивления и самоиндукции, была включена постоянная эдс Е, которая действовала неограниченное время (фиг. 3.33) и создала ток 1т.

Пусть в момент времени /==0 эта эдс внезапно исчезла, и система начала разряжаться.

Диференциальное уравнение такой системы будет

(3.56)