в ур-нии (0.22) показатель представляет собой комплексное число. Действительная часть соответствует апериодическому затухающему процессу. Все выражение в целом соответствует вектору, который вращается с частотой со, причем амплитуда его все время убывает по экспоненциальному закону.

Кривая, которая соответствует изменению тока, символически выраженному ур-нием (0.22), показана на фиг. 0.9 и называется кривой экспоненциально затухающего колебания .

§ 7. Комплексное сопротивление.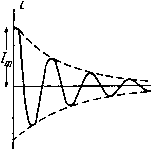

Фиг. 0.9.

Синусоидальному напряжению в линейных системах соответствует синусоидальный же ток той же самой частоты. Коэфициент, который позволяет перейти от напряжения к току, носит название сопротивления цепи

Z = -. (0.23)

Если напряжение и ток изображаются комплексными числами, то оче видно, что и частное от деления их будет также комплексным числом. Так например, пусть

тогда

(0.24)

Выражение (0.24) соответствует сопротивлению цепи. Его модуль (или амплитуда) равен

(0.25)

Его фаза равна

ср - ф == е. (0.26)

Если его изобразить комплексным числом в обычной форме, получим

(0.27)

-e>9 -(cose + /sin 6).

Вектор, изображаемый ур-нием (0.24), или комплексное число, изображаемое ур-нием (0.27), символически изображают сопротивление цепи.

Здесь снова можно повторить, что это символическое изображение отнюдь не обозначает тождественности явлений. Сопротивление вовсе не является вектором, но ему символически соответствует вектор или соответствующее вектору комплексное число.

Привычка к изображению сопротивления посредством комплексного числа в настоящее время настолько утвердилась, что первоначальное символическое происхождение этого понятия в значительной степени утратило интерес. Поэтому в теории переменного тока принято называть это сопротивление комплексным , что мы и будем делать в дальнейшем, не прибегая более ни ю каким оговоркам.

Из курса переменного тока читателю известно, что в выражении комплексного сопротивления в форме

Z = fl + /6 (0.28)

действительное число а соответствует омическому или активному сопротивлению, а мнимое число jb соответствует реактивному (индуктивному или емкостному) сопротивлению.

Пользуясь этим, мы хоим показать здесь на примере, что выбор действительного или мнимого числа для обозначения той либо другой физической величины зависит не от содержания самого физического процесса, а лишь от нашего выбора той либо другой точки зрения на природу этой ве-

-лллллл

I -J личины.

Фиг. 0.10. Рассмотрим цепь, показанную на фиг. 0.10 со-

стоящую из сопротивления R и самоиндукции L.

Если к цепи приложена эдс Е, то ток / будет

= WTh-L- (0-29)

Будем рассматривать нашу цепь как сопротивление; тогда это сопротивление будет

Z = i? + />L. (0.30)

ть нашу

Изменим теперь нашу точку зрения и будем рассматрйва цепь как самоиндукцию, которую обозначим буквой L. Тогда, очевидно, должно бцть

E = j<oL4\ (0.31)

Подставив значение / из ур-ния (0.29), найдем

t = L-/?. (0.32)

Ур-ние (0.32) показывает, что если рассматривать нашу цепь как самоиндукцию, то эта самоиндукция окажется комплексной, причем действительная ее часть определится действительной самоиндукцией цепи, а мнимая часть - омическим сопротивлением и частотой. С тем же правом можно положить, что наша цепь есть емкость С.

Тогда получили бы для определения С

i.,= o>t4-/ >?- (0.33)

§ 8. Комплексное изображение других физических величин.

Как мы только что видели, изображение физических величин при помощи комплексных чисел расширяет наши понятия и приводит к обобщению физических величин, которые первоначально представлялись как совершенно разнородные. Этим путем может быть установлен также ряд новых понятий.

Мы остановимся здесь на двух таких понятиях, а именно: на комплексной амплитуде и комплексной частоте. Положим, что в выражении

Л = AeJ (0.34)

величина Am представляет собой комплексное число. В этом случае мы

скажем, что амплитуда величины Л комплексна. Посмотрим, что это означает физически. Пусть

Am = a + jb, (0.35)

где а и 6-действительные числа. Тогда можно написать

Am = V+bQI . (0/36)

Подставив это в ур-ние (0.34), получим

А = VVi + (0-37)

Теперь амплитуда является действительным числом, но зато появился сдвиг фазы на угол arctg-, который раньше был скрыт в комплексной амплитуде.

Таким образом физический смысл комплексной амплитуды заключается в том, что -в ней Ъкрыто не только числовое значение амплитуды, но и некоторая фаза.

Пользуясь тем, что умножение на / означает поворот фазы на угол , можно преобразовать ур-ние (0.34) и другим путем, а именно :

Л = ае -f /бе = ае j уе - -J (q 38

На основании сказанного можно сделать и обратную ойерацию, т. е. скрыть сдвиг фазы в комплексной амплитуде. Например, выражение

Л = Л еЛй+9) (0.39)

где Am -действительное число), можно переписать так

д д . е . е Am (cos ср + / sin ср) е (0.40)

Обратимся теперь к частоте.

Предположим, что частота 2 представляет собой комплексную вели-

-чину

2 = 0)+/8. (0.41>

Тогда ур-ние (0.40) перепишется так

А = Am (cos ср -f / sin ср) е i-K (0.42)

Из этого выражения очевидно, в чем заключается физический смысл понятия комплексной частоты. Действительная часть ш является подлинной частотой , т. е. определяет угловую скорость периодического процесса. Мнимая же часть (или мнимая частота) определяет затухание колебаний.

Таким образом мы получаем еще одно любопытное обобщение двух величин, которые, как представлялось первоначально, не имеют между со-тбой ничего общего.