Цепь ведет себя как омическое сопротивление, если Ь = 0. Может быть три случая:

при (й = 0 (постоянный ток)

при (0 = 00 (очень высокая частота)

Z = a = Ri,

при резонансной частоте

(3.40) (3.41)

О) =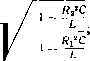

Z = a

(3.42)

и выражается ур-нием (3.38).

Если одно из сопротивлений больше волнового а другое меньше,-резонансная частота становится мнимой. При равенстве /?i = /?2

(О = -г= = (0о.

(3.43)

В контуре надо различать два тока (через емкость и через самоиндукцию)

/с=-(3.44)

Il =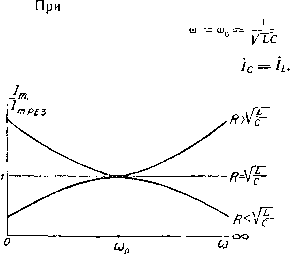

/?2 + hi

(3.45)

(3.46)

Фиг. 3.19.

YlcV

(О :

Характер кривых резонанса показан на фиг. 3.19 для трех соотношений между R и 1 = Р

На практике обычно встречаются контуры, у которых сопротивления Rx и 2 не равны друг другу. Часто принимают, что одно из них равно нулю.

Выражение для резонансной частоты в последнем случае будет иметь вид

[ - (3.47)

Л=. (3.48)

Эти выражения совпадают с найденными ранее и показывают, что резонансная частота уменьшается, когда сопротивление включено со стороны самоиндукции, и увеличивается, когда оно включено со стороны емкости.

Модуль Z при включении сопротивления в индукционную ветвь найдется из ур-ний (3.38) и (3.39). При этом полагаем /?i = 0

(3.49)

В случае включения сопротивления в емкостную ветвь (/?2=-0)

2- =

(3.50)

§ 9. Упрощение вычислений для практических случаев и пересчет сопротивлений из пучности тока в пучность напряжения или обратно.

В практических случаях весьма часто используются колебательные контуры, в которых отношение вольтампер к мощности довольно велико. Если это отношение превышает 20 или 30, т. е.

>20 или 30,

то можно для практических расчетов, не требующих особой точности упростить формулы, приведенные в двух предыдущих параграфах.

Первое упрощение касается резонансной частоты, которую в этих условиях можно определять по формуле

00 = О)

° Vlc

Второе упрощение достигается тем, что все сопротивления, включенные как парал- р тЛш Q

дельно, так и последовательно, эквивалентно

заменяют одним сопротивлением, включенным однородно с действующей в контуре эдс.

Для такой замены действительное сопротивление пересчитывается следующим образом. Фиг. 3.20.

Пусть, например, в контуре эдс Ё включена параллельно конденсатору, а сопротивление R последовательно (фиг. 3.20). Принимаем, что резонансная частота контура равна

Мощность, выделяемая в сопротивлении R, равна

Р -hll

Значение 1т определяем из равенства

1т - EmOiC.

Подставив взамен со для частоты резонанса

получаем

Отсюда мощность равна

=я /:.

IR BCR

2 - 2L (3.51)

Теперь находим такое сопротивление г, в котором при включении параллельно конденсатору выделится такая же мощность.

По закону Ома такое сопротивление удовлетворяет равенству

(3.52)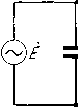

F 2

Сравнивая ур-ния (3.51) и (3.52; видим, что

(3.53)

Фиг. 3 21.

Таким образом взамен контура фиг. 3.20 можно применить контур фиг. 3.21. Вблизи резонанса он эквивалентен контуру фиг. 3.20.

Обратно, если бы первоначально сопротивление было включено параллельно и имело величину г, его мокно было бы заменить последова-

ЭПВИВЙЛЕНТНО

Фиг. 3.22.

тельным сопротивлением, воспользовавшись такой же формулой пересчета {фиг. 3.22),

Часто сопротивление включается, как показано на фиг. 3.23, т. е. шунтирует некоторую часть самоиндукции.

Это включение также ожно эквивалентно заменить параллельным или последовательным включением.

Вычисление имеет простой характер, если ответвляющийся в сопротивление ток мал по сравнению с током, идущим по самоиндукции.

Если участок самоиндукции, к которому присоединено сопротивление г имеет индуктивное сопротивление а полное сопротивление ка-

тушки равно /coL, то амплитуда напряжения на сопротивлении г меньше, чем амплитуда напряжения на всей катушке самоиндукции в - раз. 1

Фиг. 3.23.