Равенства (3.20) показывают, что кривая резонанса имеет минимум, т. е. форма ее в общих чертах должна иметь характер кривой АВ фиг. 3.15. Теперь положим, наоборот, что

Тогда при

гпрез

V LC

ТОК через источник будет значительно больше, чем ток через сопротивления и Гз, и в основном образуется за счет тока, идущего через емкость и само-индукцию.

Поэтому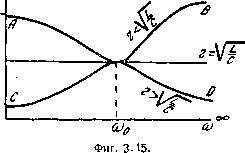

при О)

Т. е.

У LC

Поэтому теперь для определения кривой резонанса получаем следующие три положения:

при >- при со -

при Сй =

V LC

1т -

(3.21>

Кривая резонанса имеет максимум. Вершина кривой тем больше выделяется, чем больше сопротивление г по сравнению с mL и т. е. чем

больше реактивная слагающая тока по сравнению с активной. Поэтому кривая будет тем острее, чем больше отношение вольтампер к мощности. Общий вид кривой соответствует кривой CD фиг. 3.15. Наконец, если

сопротивление цепи при условии

Y LC

окажется равным г, т. е. всем трем значениям со будет отвечать один и тот же ток

т т

1т--г

§ 7. Математическое исследование итого случая.

Полное сопротивление цепи можно представить как сумму двух сопротивлений

Z = Zi-fZ2, (3.22)

Z,= -

(3.23) 117

Отсюда Z получается в виде комплекса

(3.24) (3.25)

(3.26)

Сопротивление контура становится чисто активным, когда 6=0. Для этого должно быть

-L l/

-{tJ

(3.27)

Искомая частота становится мнимой, если одно из сопротивлений больше, а другое меньше волнового сопротивления контура.

Это показывает, что сопротивление контура в этом случае не может быть чисто активН)Ым ни при какой частоте.

Если Г1 = Г2 = г, то

(3.28)

/ LC

в этом случае при резонансной частоте

а = 2

6 = 0

(3.29)

Если одно из сопротивлений, например г, отсутствует вовсе, то его надо положить равным бесконечности. При Г1 = сх> резонансная частота

(О = COq j/ 1

Эта частота меньше o - jx: При Г2 = оо резонансная частота

(О = (О,

Сг 2-

(3.30)

(3.31)

больше, чем (Оо=/ .

Модуль Z при включении сопротивления со стороны конденсатора найдется из ур-ний (3.25) и (3.26), полагая = оо

2 1

(3.32)

ири включ[ении сопротивления со стороны самоиндукции надо положить = со. Тогда

В первом случае (фиг. 3.16) при ш==0,

(3.33)

(3.34)

Другими словами, постоянный ток проходит по катушке L, как по короткому замыканию, и далее по сопротивлению г,. При со = оо конден-

>

о! 3

Флт. 3.16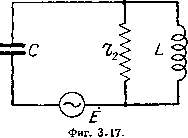

саторная цепь является коротким замыканием, но самоиндукция L представляет собой бесконечное сопротивление; поэтому

Z = оо.

Во втором случае (фиг. 3.17) при ш = 0

2 = оо,

так как конденсатор не пропускает постоянного тока. При со = оо

(3.35) (3.36) (3.37)

так как конденсатор является коротким замыканием, а индуктивное сопро-тивление, шунтирующее утечку, бесконечно велико.

§ 8. Комплексное сопротивление и кривые резонанса для случая, когда эдс включена в контур параллельно, а сопротивление последовательно.

В случае схемы фиг. 3.18 комплексное сопротивление контура для эдс Ё определится следующим выраже-

Z = а-\- jb, р1 ддддд-

нием где

J; (3.38)

(3.39)

-\АЛЛЛЛ-

Фиг. 3.18.