
 |
|
|
Главная -> Основание неперовых логарифмов Легко видеть непосредственно из схемы фит*. 3.11, что ток, проходящий через источник, состоит из двух слагаемых. Одно слагаемое представляет собой ток через сопротивление г. Этот ток при постоянной амплитуде Ет одинаков для всех частот и равен 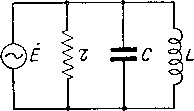 Второе слагаемое образуется током, идущим через контур. При настройке в резонанс, т. е. когда Фиг. 3.11, у LC контур является бесконечным сопротивлением (в установившемся режиме) и ток равен нулю. При частотах выше резонансной контур эквивалентен емкостному сопротивлению, так как разность становится положительной; положительная же реактивная проводимость есть емкостная проводимость. Соответствующая эквивалентная схема всей цепи показана на фиг. 3.12. При частотах, меньших резонансной, эквивалентная схема будет иметь вид фиг. 3.13. 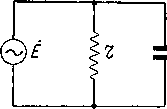 Фиг. 3.12. Фиг. 3.13. Это, впрочем, можно заключить также непосредственно из ссемы контура, так как очевидно, что при резонансе ток через емкость равен току через самоиндукцию; при частотах выше резонансной будет преобладать ток через емкость, а при частотах ниже резонансной - ток через самоиндукцию, чем и определится знак реактивной слагающей тока, идущего через источник эдс Е, При очень больших частотах емкость С явится почти коротким замыканием, а при очень малых частотах, наоборот, самоиндукция L явится почти коротким замыканием. В обоих случаях ток в цепи источника будет весьма значителен. Таким образом, кривая резонанса имеет минимум при и уходит в бесконечность при V LC ш = О (О = оо. сравним выражения для комплексного сопротивления контура при последовательных сопротивлениях эдс и комплексной проводимости при параллельных сопротивлениях и эдс, т. е. (3.18) Оба выражения одинаковы по фоме. Второе выражение может быть получено из первого, если сопротивления заменить проводимостями, как это видно из следующей таблички. Таблица Ifl.I
Соответствие в явлениях выражается следующей таблицей. Таблица ШЛ Последовательное включение Параллельное включение При резонансе ток максимален и равен При частотах выше резонансной реактивное сопротивление становится индукционным. При частотах ниже резонансной реактивное сопротивление становится емкостным. Чем меньше отношение тем острее кривая резонанса. Чем меньше отношение тем бодьше вольтамперы по сравнению с мощностью. При резонансе ток минимален и равен т Г При частотах выше резонансной реактивное сопротивление становится емкостным. При частотах ниже резонансной реактивное сопротивление становится индукционным. Чем меньше отношение тем острее кривая резонанса. Чем меньше отношение тем больше вольтамперы по сравнению с мощностью. Чем больше вольтамперы по сравнению с мощностью, гм острее кривая резонанса. § 6. Физическая картина при последовательном включении эдс и параллельном включении сопротивлений. Рассмотренные выше способы включения эдс и сопротивления называются однородными включениями (оба параллельно или оба последовательно). Более сложными случаями являются те, при которых сопротивление и эдс включены неоднородно. Все исчисления в этом случае делаются так же, как и в случае однородного включения, но они оказываются довольно громоздкими. Поэтому ниже приведены окончательные результаты без выводов. Сами выводы (за исключением громоздкости) не представляют ничего трудного. Предварительно же посмотрим чисто качественно, каких явлений можно ожидать в этом случае. На фиг. 3.14 приведена схема, в которой источник эдс Е включен в контур последовательно, а по обеим сторонам его включены сопротивления Г1ИГ2. Первое - параллельно емкости С, второе - самоиндукции L. Прежде всего ясно, что при частоте ш->-оо емкостное сопротивление, шунтирующее Tl, стремится стать коротким замыканием. При этих же условиях индуктивное сопротивление самоиндукции L стремится к бесконечности, и сопротивление Га оказывается ничем не шунтированным. Поэтому при ш-оо сопротивление, нагружающее источник, стремится к величине Гд. Наоборот, при ш->-0 (т. е. при весьма низких частотах) самоиндукция превращается в короткое замыкание, шунтирующее Гд, а сопротивление емкостного шунта у становится очень большим и поэтому не играет роли. Полное сопротивление цепи определяется величиной г-. Для того, чтобы выяснить, каково будет сопротивление цепи при средних значениях ш, положим для простоты, что Г1 = Г2 = Г X SI, Фиг. 3. 4 и что (3.19) Если положить Ш = то вследствие соотношения (3.19) Поэтому можно пренебречь емкостным и индуктивным токами и считать, что весь ток, проходящий через источник, образуется за счет тока, идущего через сопротивления ц г. Тогда сопротивление цепи будет равно Таким образом мы нашли три точки, определяющие форму кривой резонанса, а именно: при (0 = 00 при (0 = 0 при (0 = V LC
|