Поэтому отношение будет близко к единице даже при сравнИ

т рез

тельно значительной расстройке.

Если же, наоборот, R очень мало, то достаточно самого небольшого изменения о, С или L, чтобы член

получил большое значение, а следовательно, отношение резко умень-

m рез

ШИЛОСЬ бы.

С другой стороны, быстрое или медленное возрастание разности

(3.6)

зависит от соотношения между L и С.

Для того, чтобы выяснить этот вопрос, представим то же выражение (3.6) следующими двумя способами путем подстановки

(coL-±)=L(.-),

(3.7) (3.8)

Выражение (3.7) показывает, что

при изменении (о разность {L -

растет тем быстрее, чем больше L, а выражение (3.8),- что она растет тем быстрее, чем меньше С. Поэтому ординаты кривой резонанса тем быстрее

убывают вблизи частоты резонанса, чем больше величина ~ и чем меньше R.

На фиг, i3.7 показаны две кривые резонанса. Тупая кривая (верхняя) соответствует большей величине, а острая кривая - малой величине отношения

Фиг. 3.7, L

Величина имеющая размерность сопротивления, называется ха-

рактеристичным сопротивлением контура .

§ 3. Сдвиг фазы между эдс и током.

Кроме кривой резонанса контур может быть еще охарактеризован кривой изменения сдвига фазы между эдс и током в зависимости от частоты со.

при частотах, меньших резонансной, разность (wL - полозкптелыГа,

и контур (в установившемся режиме) является эквивалентом самоиндукции, соединенной последовательно с омическим сопротивлением (фиг. 3.8). При частотах, больших резонансной, он, наоборот, эквивалентен емкости, соединенной с омическим сопротивлением (фиг. 3.9).

Угол сдвига фазы при резонансе равен нулю, а при больших значениях выражения

(определяющего тангенс угла сдвига) становится близким к 90°.

-ЛЛЛЛЛЛЛЛЛг

-AA/VWWV

о

Фиг. 3-8.

Фиг. 3.9.

На фиг. 3.10 показан тип кривых ср =F. По ординатам отложен уголср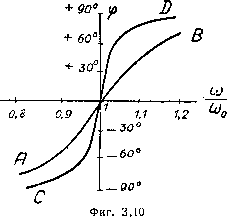

в градусах, а по абсциссам - отношение -. Кривая АВ соответствует большой

величине

а кривая CD - малой.

Первая кривая вблизи частоты идет более полого, а вторая более круто. Причины этого совершенно те же, что и причины, влияющие на степень остроты кривой резонанса.

§ 4. Вольтамперы и мощность в контуре, настроенном в резонанс, при последовательно включенных эдс и сопротивлении.

Напряжение на конденсаторе Ёс контура найдется, если помножить ток на емкостное сопротивление конденсатора. Так что

Eo = -j- (3.9)

В момент резонанса

поэтому

R

Ёс-i

RioC

(3.10) (3.11)

Множитель - / показывает, что напряжение на конденсаторе сдвинуто на 90° по отношению к эдс Ё, а следовательно, и к току /, который в момент резонанса совпадает по фазе с эдс.

Йз этого следует, что когда электрический заряд в конденсаторе достигает своего максимума, магнитное поле равно нулю и обратно.

в кОнтуре происходит, таким образом, два процесса. С одной стороны, в нем циркулирует некоторая энергия, которая переходит из электрической формы в магнитную, и обратно. С другой стороны, в сопротивлении выделяется некоторая активная мощность.

Чтобы сопоставить эти два явления, вводят понятие реактивной мощности , которую определяют для единообразия с активной мощностью следующим образом.

Активная мощность

Ра= (3.12)

может быть при резонансе определена как произведение

Р = 5. (3.13)

Аналогично этому реактивной мощностью, или правильнее вольтампе-рами контура, называют величину

Р,= ?-. (3.14)

Это выражение можно написать е*ще следующим образом. Имея в виду,

получим ИЗ ур-ния (3.14) откуда получаем

Pr=Irr?}/~, (3.15)

(3.16)

ур-ние (3.16) показывает, что реактивная мощность в контуре тем больше по сравнению с активной, чем больше характеристическое сопротивление контура по сравнению с активным сопротивлением, включенным лоследовательно.

Теперь мы можем сформулировать результаты, полученные в предыдущем параграфе, следующим образом.

Кривая резонанса контура тем острее, а фазовая кривая тем круче, чем больше вольтамперы в контуре по сравнению с мощностью.

Это правило следует запомнить. Оно оказывается более общим, чем приведенное ранее, и в равной степени годится и для других случаев вклю--чения сопротивления.

§ 5. Комплексное сопротивление и кривая резонанса для случая, когда эдс и сопротивление включены параллельно контуру.

Рассмотрим теперь случай, когда сопротивление г и эдс Е включены параллельно контуру. Соответствующая схема показана на фиг. 3.11.

Комплексная проводимость, которую представляет собой контур для эдс Ё, определится формулой

-j- = l+/(o,C-i). (3-17)