ГЛАВА II .

КОЛЕБАТЕЛЬНЫЙ КОНТУР.

ОБОЗНАЧЕНИЯ К ГЛ. HI

С - емкость

с - скорость света Е,е- напряжение

е -основание неперовых логарифмов

/ - циклическая частота

g - активная положительная проводимость /, i - сила тока

/ -мнимое число (оператор по-

ворота вектора на угол-

L - коэфициент самоиндукции In - натуральный логарифм Р - мощность R,r - активное (ваттное) положительное сопротивление Т - период t - время

У - реактивная проводимость

Z -комплексное выражение кажущегося сопротивления (Z=r-+-yx)

2 - кажущееся (полное) сопротивление (модуль) о - коэфициент затухания контура

О- логарифмический декремент затухания в контуре

X - длина волны р -волновое сопротивление и> - круговая частота и>о-сокращенное обозначение вели-1

чины --

Y LC

= - знак тождества. Выражен. {a-{-b)zL - с означает: обозначим {а-\-Ь) через с .

Амплитудные значения переменных величин обозначены большой буквой с индексом т, например, Е, 1, Р

и т. д.

Постоянные и среднеквадратичные значения теми же буквами без индекса, например, Е, 1, Р и т. д.

Мгновенные значения, выраженные в тригонометрической форме, обозначены малыми буквами, например, i =Ism (Ы) и т. д.

Мгновенные значения, выраженные в комплексной форме, обозначены большой буквой с точкой наверху, например,

/ = а + = £ е + f и пр.

§ 1. Простой колебательный контур.

Соединение сосредоточенных емкости и самоиндукции (фиг. 3.1), как было уже сказано, называется колебательным контуром. Колебательный контур является одним из наиболее важных и часто встречающихся элементов радиотехнических устройств.

В каждом колебательном контуре всегда есть источники потерь, превращающие часть энергии в тепло. Обычными источниками потерь являются сопротивления проводов, утечки в изоляции и потери в диэлектриках. Кроме того, если контур связан с другими цепями, то он может также отдавать этим цепям часть циркулирующей в нем энергии.

Все эти потери можно заменить некоторыми эквивалентными утечками или последовательно включенными сопротивлениями. Без большой погрешности можно также сопротивления и утечки, распределенные в различных участках самоиндукции и емкости, объединить в одно или два места и рассматривать их как сосредоточенные сопротивления и утечки.

В линиях этого нельзя было сделать вследствие того, что ток и напряжение различны в различных точках линии. В контуре же, поскольку мы принимаем L и С за сосредоточенные, мы этим самым принимаем, что по всей самоиндукции ток одинаков, а у конденсатора напряжение между обкладками всюду одинаково. Возможность таких допущений значительно упрощае\ исследование явлений в контуре.

Ф.1Г. 3.1.

простейшими способами включения сопротивлений являются показанные на фиг. 3.2 и 3.3. Первый способ называется последовательным, а второй- параллельным включением.

Эдс может быть включена в контур различными способами или появляться вследствие индукции в различных частях контура.

Фиг. 3.2.

Фиг. 3.3.

Простейшими случаями включения эдс является параллельное включение (которое taкжe называется включением в пучность напряжения), показанное на фиг, 3.4, и последовательное включение, показанное на фиг. 3.5. Последнее называется также включением в пучность тока.

При исследовании явлений мы будем считать, что источник эдс, включенный параллельно, не создает никакой утечки, а источник эдс, включенный последовательно, не создает никакого сопротивления в контуре.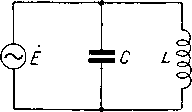

Фиг. 3.4.

Фиг. 3.5

Указанные два простейших способа включения сопротивлений (последовательное и параллельное) и два способа включения эдс (последовательное и параллельное) приводят к возможности получения четырех основных (или простейших) комбинаций работы источника на контур, которыми мы прежде всего займемся в условиях установившегося режима.

§ 2. Комплексное сопротивление и явление резонанса в контуре, \ когда эдс и сопротивление включены последовательно.

На фиг. 3.6 показана схема включения эдс Ё и сопротивления R в кон-

тур последовательно .

Сопротивление контура в этом случае, как легко видеть, равно

при помощи этого выражения определяем ток в контуре

(3.1)

ЛЛЛЛЛЛг

Фиг. З-б.

Освободившись от мнимости в знаменателе, приведем это выражение к виду

найдем

1 \2

(3.2)

т. е.

Угол сдвига между током и действующей в цепи эдс

ср = агс tg(-),

Если

ТО сопротивление контура становится чисто активным и равным R, так как

Угол сдвига между током и эдс также равен нулю.

Частота, удовлетворяющая этому условию, называется резонансной частотой. Резонансную частоту мы будем отмечать нулевым индексом (Hq.

Изменяя емкость или самоиндукцию контура, можно настроить контур на ту либо другую резонансную частоту.

Ток в момент резонанса будем отмечать индексом рез (например, /отрез). Так как при резонансе сопротивление минимально, то ток максимален.

Кривая, показывающая отношение амплитуды тока в контуре, при какой-нибудь частоте (о к амплитуде при р.езонансе, носит название кривой резонанса .

Легко вывести, что кривая резонанса выражается следующим уравнением

1т 3= /~-

т рез I /

/от рез I / (wL -

(3.4)

Она имеет максимум, равный единице, когда

(.1-) = 0.

Дальнейший ход ее зависит от соотношения между величинами L, С и R. Без сложных вычислений легко видеТь, что если/? очень велико, то член

(3.5)

в ур-нии (3.4) будет мал даже при значительной величине разности 110