Поэтому отаошенйе -7 и определяет быстроту спада кривой, т. е.

остроту ее вершины. Чем больше это отношение; тем медленнее происходит спад, т. е. тем более тупой вид принимает кривая резонанса. Если

=- = 00, кривая будет параллельна оси абсцисс (кривая i?i = р на фиг. 2.20).

§ 23. Явление резонанса в двухпроводноЦ линии при включении сопротивления в пучность напряжения.

Рассмотрим теперь такую же линию, но предположим, что сопротивление г включено на ее конце, противоположном точке включения источника, как показано на фиг. 2.21. Здесь надо рассмотреть три случая: а) когда

/ >/ , б) когда <у§ и, наконец, в) когда г=ур. Начнем с последнего случая.

Так как линия замкнута на активное сопротивление, равное волновому, то в ней установится бегущая волна йезависимо от ее длины и от частоты.

Амплитуда /тока будет

1т,--(2.120)

/7 S7

кривая резонанса получит вид, по-

казанный на фиг. 2.20 для случая р. Положим теперь

Фиг. 2.21.

Явление будет приближаться к случаю линии, разомкнутой на конце (с той только разницей, что кроме стоячей волны, будет еще бегущая волна, как это было выяснено в § 12), В момент резонанса цепь будет

эквивалентна, если не короткому замыканцю для эдс Е (лак было бы в случае линии, разомкнутой на конце), то некоторому небольшому сопротивлению, которое назовем R.

Чтобы вычислить значение /?, поступим так. Посмотрим прежде всего, какая мощность расходуется в сопротивлении г в момент резонанса. Амплитуда напряжения на конце линии равна

ЕтА=1то\/ ~. (2.121)

Следовательно, мощность в сопротивлении г равна

р-- = . (2.122)

Очевидно, что сопротивление /? должно удовлетворять требованию эквивалентности, т. е. мощность, выделяемая в нем при амплитуде тока /те, должна равняться Р.

Так что

2г 102

mQ f> ft D

=Ц?. (2.123)

Отсюда

Итак, в момент резойанса амплитуда тока будет равна

/дао -

-то R

(2.124)

(2.125)

При отступлении от резонанса появятся индуктивные слагающие сопротивления, и ток станет меньше.

Кривая резонанса, соответствующая этому случаю, имеет, следовательно, характер кривых фиг. 2.20, например, для и R.

Наконец, третий случай, когда

приближается к случаю, когда линия на конце замкнута накоротко. Если бы г было равно нулю, то цепь явилась бы при резонансе бесконечной самоиндукцией и ток Imo был бы равен

нулю. Но на самом деле в линии существует бегущая волна, питающая сопротивление г. Поэтому дело происходит так, как будто в цепь источника эдс включено эквивалентное сопротивление, вычисляемое по той же ф-ле (2.124)

Следовательно, в момент резонанса ток не равен нулю, и его амплитуда равна

1.2 1 0.8 0.6 ОЛ 0,2

(2.126)

4 5

0 12 Фиг. 2.22.

3 4 1Z

и поэтому общее сопротивление падает.

При отступлении от резонанса сама линия перестает быть бесконечным сопротивлением, а амплитуда тока растет.

Кривая получает вид, показанный на фиг. 2.22.

Два частных случая, которые мы уже здесь затронули, представляют особый практический интерес и их следует заметить. А именно:

1) если г = 0, схема при резонансе получает вид фиг. 2.23а. Она представляет собой участок линии, коротко замкнутой на конце, и эдс Ё вклю-

.-/ Д-. --1-

Фиг. 2.23 а.

Фиг. 2.236.

чена в пучность напряжения. Сопротивление такой линии для эдс Ё равно бесконечности, т, е. линия эквивалентна полной изоляции;

2) если г - оо, ли1?ия оказывается разомкнутой на конце и эквивалентна

короткому замыканию для эдс Ё (фиг. 2.23),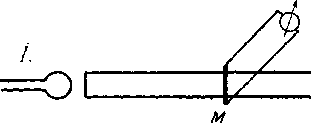

§ 24. Линия как волномер.

Явление резонанса в линии используется для определения частоты источника эдс или, вернее, для определения волны, соответствующей этой частоте. Для этого с источником связывают, например, при помощи взаимной индукции двухпроводную линию (называемую в этом случае лехеровой системе й ). На линии делается подвижной контакт, замыкающий накоротко

оба провода. Этот контакт называется мостом и на фиг, 2.24 обозначен буквой М. С мостом связывают измерительный прибор, показывающий присутствие тока в мосте и позволяющий судить об его относительной величине. Обыкновенно для этой цели Фиг 2 24 применяют термоэлемент, пи-

тающий гальванометр.

Передвижение моста настраивает линию. Когда мост находится в таком положении, что линия оказывается в резонансе с частотой эдс - ток в гальванометре достигает максимального значения. Положения резонанса повторяются через расстояния, равные половине длины волны. Находят несколько таких положений. Иггервалы между ними позволяют измерить длину полуволны непосредственно измерительной линейкой. Этот способ (практически, разумеется) можно применять только для волн, длина которых не превышает нескольких метров. Это так называемые короткие и ультракороткие волны. Для измерения более длинных волн применяются приборы, с которыми мы познакомимся ниже.

§ 25. Графики распределения тока и напряжения.

Участок линии длиною /, замкнутый на конце накоротко, представляет, как мы видели, систему, настроенную в резонанс с частотой

2 НС

В процессе колебаний пучность тока находится у короткозамкнутого конца, а пучность напряжения у открытого конца. Распределение амплитуд тока и напряжения вдоль такого

участка линии может быть изображено , г

графиком фиг. 2.25. J/rjj Jl

Жирной линией BACD изображен------ -

провод. Пунктирные линии сверху и . -

снизу дают распределение тока и на- пряжения. Расстояние этих пунктирных линий от жирных линий в условном мае- штабе соответствует амплитудам тока

и напряжения. / - --

Согласно сказанному ранее о сто- дгх

ячей волне в проводе эти линии пред- Ф 25

ставляют собой участки-синусоид. Ли-НИИ, находящиеся выше АВ, дают положительное значение амплитуд, существующих в проводе АВ, а линии, находящиеся ниже CD, дают значения амплитуд в проводе CD, причем эти амплитуды отложены вниз, что соответствует отрицательным амплитудам . Этим условно выражается противоположность фазы.