не соблюдено, то волновое сопротивление может иметь иную величину. В частности, когда оба провода колеблются в фазе и образуют, таким образом, один провод из двух жил, то в присутствии проводящей земли, которая служит обратным проводом системы, волновое сопротивление будет

р = ЪО\п ОМ,

(2.113)

высота проводов над землей, причем и h<k.

Для линии, состоящей из двух коаксиальных цилиндров, показанной в разрезе на фиг. 2.17,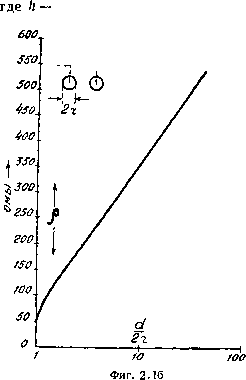

где Гз - радиус внутренней поверхности внешнего цилиндра, а - наружный радиус внутреннего цилиндра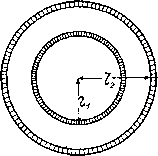

Фиг. 2.17.

§ 22. Явление резонанса в двухпроводной линии при включении сопротивления в пучность тока.

Возьмем участок линии длиною I и включим на одном его конце источник 0 с частотой и последовательно с источником - сосредоточенное сопротивление R, фиг. 2.18. Если

показано на длина волны источника, т. е. величина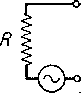

равна четырем /, линия представляет собой эквивалент конденсатора бесконечно большой емкости, и является Фиг. 2.18 вследствие этого коротким замыканием для переменного тока. Поэтому цепь источника Eq оказывается замкнутой на сопротивление R. Ток в месте включения источника будет, следовательно,

Амплитуда тока

/о==

то

(2.114)

(2.115)

На конце линии А ток будет равен нулю, но зато здесь будет максимальная амплитуда напряжения, которая, как ясно из предыдущего, определится величиной

-шА - то I/ Q

(2.116)

Теперь будем менять частоту, давая ей значения (ш), большие и меньшие частоты 0).

При частотах, меньших шц, длина волны будет больше Хц, и линия представит собой некоторое емкостное сопротивление, значение которого определится выражением

fc= ?:<tg(f/).

Поэтому амплитуда тока в месте включения источника станет

(2.117)

/то -

(2.118)

Это уравнение показывает, что амплитуда тока меньше, *1ем в случае О) = (1)0. Она будет все более уменьшаться по мере роста С, т. е. по мере уменьшения частоты а>.

Если частоту сделать, наоборот, большей чем (о, волна станет меньше, чем 41, и линия превратится в эквивалент самоиндукции.

Индуктивное сопротивление выразится тем же ур-нием (2.117) с противоположным знаком и будет расти по мере увеличения а амплитуда тока /ото и амплитуда напряжения Етл будут уменьшаться.

Положение, при котором ш = <о, т. е.

= 4/,

называется положением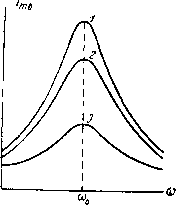

Фиг. 2.19.

меньшему, а кривая 3-зумеется от величины

резонанса и характеризуется тем, что для эдс Ё цепь превращается в чисто активную нагрузку R.

Достигнуть положения резонанса можно,либо изменяя частоту ш, либо, оставляя эту частоту постоянной, изменять длину линии. Эта операция называется настройкой цепи .

Признаком резонанса в данном случае является достижение током 4 или напряжением Ёа максимальной амплитуды.

Изменение амплитуды тока Iq в зависимости от изменения частоты или от изменения настройки (длины) линии может быть выражено графически в виде кривой.

На фиг. 2.19 даны три примерных кривых, дающих зависимость

/то = /<< )

для одной и той же линии, но при трех разных сопротивлениях R. Кривая 7 соответствует большему сопротивлению. Эти кривые зависят ра-EmQ. В данном случае для всех трех кривых при-

менена одна и та же величина Ето- Однако для того, чтобы можно было сравнить форму этих кривых независимо от приложенной эдс, их строят обычно следующим образом.

По оси абсцисс откладывают либо частоту, либо отношение частоты к частоте резонанса а>о, либо отношение По оси ординат отклады-

вают отношение амплитуды тока при данной частоте к амплитуде при резонансе, либо квадраты этих величин.

В таком виде эти кривые называются кривыми резонанса и являются важной характеристикой как участка линии, так и других цепей.

о Фиг. 2.20.

RfO.Odp

cj-u).

slxloo

Ha фиг. 2.20 приведены три такие кривые резонанса. Эти три кривые соответствуют длине с волновым сопротивлением р, но различным сопротивлениям R, включенным в пучность тока,

Ri = 9\ /?2 = 0>3р; /?з = 0.03р.

По абсциссам отложено значение tnJ а по ординатам .

Полезно отдать себе отчет, отчего при меньшем сопротивлении кривая имеет более узкую вершину и более крутые скаты.

Дело здесь в следующем. В момент резонанса амплитуда тока определяется формулой

При отступлении от резонанса в знаменатель входит либо

Чем быстрее нарастает величина a>L или при изменении частоты, тем

круче будет падать кривая. Наоборот, чем больше R, тем падение будет медленнее, так как добавок индуктивного напряжения меньше сказывается на величине полного сопротивления. Как известно, индуктивная слагающая, которую запишем так

(2.119)

прямо пропорциональна величине волнового сопротивления.