Эти уравнения показывают, что для того, чтобы найти, например, напряжение в точке х, надо напряжение в конце линии увеличить по амплитуде на величину радикала и сдвинуть по фазе на угол Углы ф и ср определяются выражениями:

tg<l>=.th(px)tg(ax), (2.102)

tgcp = cth(px)tg(ax).

tg(cp-t)

sin (2ax)

sh (2px)

(2.103) (2.104)

Из ур-ний (2.100) - (2.104) можно сделать следующие выводы: 1) Ток и напряжение растут от конца провода к началу, вследствие непрерывного возрастания ch(2px). Одновременно с этим они испытывают периодические изменения амплитуды вдоль длины провода вследствие вли-яниячлена cos(2ax).

Если р мало и ch (2х) растет медленно, то можно принять, что максимальное значение амплитуды напряжения имеет место при cos(2ax)=l

или х = 0, , X... При этих же значениях х амплитуда тока проходит

через минимум, не достигая однако нуля, так как ch (2рх)>1. Наоборот, при cos(2ax) = - 1 амплитуда напряжения проходит через минимум, а ампли-

3,5,

туда тока через максимум; при этом х = --, - к, -к и т. д.

В действительности возрастание ch(2px) сдвигает несколько максимум в сторону начала фидера, а минимум в сторону конца фидера, заметно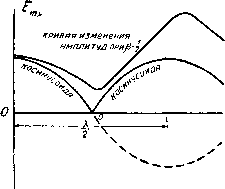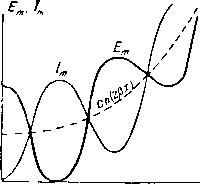

2/JX

Фиг. 2.14.

Фиг. 2.15.

искажая синусоидальный характер распределения только в том случае, если затухание велико, как это, например, показано на фиг. 2.14, где верхняя кривая

дает распределение потенциала при большом затухании f р= , а нижняя

кривая-нормальную косинусоиду.

Общий характер изменения амплитуд тока и напряжения вдоль фидера показан на фиг. 2.15.

2) Угол сдвига фазы напряжения изменяется вдоль фидера. Чтобы выяснить характер этого изменения, положим р=0, что соответствует фидеру без потерь, тогда угол ф=0, или к, т. е. напряжение в различных точках фидера или в одинаковой фазе или в противоположной фазе с напряжением на концах. Это - случай чисто стоячей волны. С другой стороны, если рх достаточно велико, так что можно написать th (рх) 1, то ф = ах. Последний случай соответствует бегущей волне, и угол сдвига фазы изменяется пропорционально изменению координаты х. При О <th (рх) < 1 получится некоторое промежуточное изменение фазы вдоль фидера, которое у конца (при х = 0) близко к случаю стоячей, а на достаточно большом расстоянии от конца th(px) 1 близко к случаю бегущей волны.

Сдвиг фазы тока относительно фазы напряжения при малых значениях

близок к 90°, так как th ( р - S , и, следовательно, ср

shco)

При X = 2 Т * s* (*-) получает поочередно значение -1, -f-l, -1,... и т. д., вследствие чего через каждые четверть волны опережение фазы сменяется запаздыванием и, наоборот, как при чисто стоячей волне. Напротив, при большом значении х величина sh(px) становится значительной и (9 - приближается к нулю. Сдвиг фазы между током и напряжением исчезает, и картина приближается к картине чисто бегущей волны.

Кажущееся сопротивление фидера от точки х до конца найдется из ур-ний (2.98) и (2.99).

Z. = =

ch(/ax + рх) Ch (gx) COS (ах) + / sh (х) sin (ах) sh (/ах + рх) sh (рх) COS (ix) + / ch (?x) sin (зх)

Освободившись от мнимости В знаменателе, получим У ch фх) sh фх) - / cos fax) sin (ах)

(2.105)

(2.106)

sh2 (х) C0S2 (ах) 4- ch2 (pxj sin (ах)* Мнимая часть проходит через нуль каждый раз, когда

ах = 0, , у... и т. д.

при этих значениях сопротивление становится чисто активным. При больших значениях х можно положить

Тогда

ch (px) = sh фх).

. cos (ах) Sin (ах)

ch? (pxj

(2.107)

Ввиду того, что при этих условиях сЪ.фх)!, можно пренебречь реактивной частью сопротивления и тогда Zx = ?, т. е. в начале фидера при достаточной его длине сопротивление практически равно волновому.

3) Мощность, теряемая на участке фидера между его концом и точкой х,

Р, = 5фС05(ср-ф),

(2.108)

где Етх и 1тх-амплитуды; так как

tg(cp ) =

sin (2з(х) Sh (7

COS2(cp - ()

sh2 (2 Эх)

1 -1- tg2 (ср - .L) sin (22Х) -I- sh2 (2x) * Из ур-ний (2.100) -(2.104) и (2.109) находим

£2.

(2.109)

(2.110)

Имея в виду, ЧТО ch (2рх) - sh (2рх) = 1, легко видеть, что выражение, стоящее в прямых скобках под знаком корня, равно единице; поэтому

fsh(2px).

(2.111) 97

§ 20. Замечание о применимости полученных результатов только к установившемуся режиму.

Предпосылка, которую мы раньше приняли при решении диференци-альных уравнений, заключалась в том, что ток и напряжение во всех точках линии подчиняются синусоидальному закону. Эта предпосылка выражает собой предположение, что режим установился. Решение получилось в форме уравнений, соответствующих двум системам волн, движущимся навстречу одна другой, и дающих в сумме те либо другие токи и напряжения в каждой точке линии. Эта картина соответствует действительному физическому процессу и из нее вытекает следующее очень важное следствие.

Отраженная волна не может возникнуть раньше, чем прямая волна не дойдет до конца линии. свою очередь отраженная волна дойдет до начала линии только спустя некоторый промежуток времени, в течение которого она движется. Затем в число прямых волн могут войти также волны, которые отразились от источника, дойдя до точек включения источника. Эти, так сказать, вторичные прямые волны, в свою очередь дойдя до конца линии, произведут отражейные волны.

Та картина, которая дается написанными формулами, относится таким образом к завершившемуся процессу.

В самый первый момент и до тех пор, пока придет первая отраженная волна, всякая линия (а следовательно, и всякий конденсатор или самоиндукция) представляют для источника чисто активную нагрузку, сопротивление

которой определяется величиной

Активная слагающая остается во все время, пока процесс устанавливается и пока в цепи накапливается некоторая энергия, в виде электромагнитного поля стоячей волны.

Таким образом все написанные формулы относятся к установившемуся режиму.

§ 21. Формулы для определения параметров некоторых линий.

Для всех однородных воздушных линий с малыми потерями, практически, справедливо соотношение.

где с - скорость света.

Для двухпроводной воздушной линии, подвешенной далеко от земли,

4 In -

гн/см.

9- ЮОС;

Здесь d -расстояние между центрами проводов; г - радиус провода; In - натуральный логарифм. Отсюда

Р = /~=120\п jOM. (2.112)

Обычно волновое сопротивление двухпроводной линии бывает от 100 до 600 ом. На фиг. 2.16 дан график зависимости волнового сопротивления от расстояния между центрами проводов и радиуса проводов, соответствующий этой формуле.

Ур-ние (2.112) написано в предположении, что провода фидера колеблются в противоположной фазе и имеют разные токи. Если это условие