Таким образом комплексное число

соответствует вектору А (фиг. 0.5), являющемуся сумйой вектора а и перпендикулярного ему вектора Ь. Длина (или амплитуда) вектора равна УФ-\-Ъ,

а угол б определяется дугой, тангенс которой равен -т. е.

8 = arctg4-

(0.8)

Здесь опять следует обратить внимание, что вектор А отнюдь не отождествляется с комплексным числом, а между ними устанавливается определенное соответствие, в силу которого каждому вектору соответствует комплексное число, и наоборот.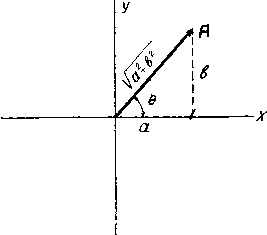

Фиг. 0.5.

Теперь взамен тока или напряжения, выраженных тригонометрической функцией, мы можем написать соответствующее комплексное число и, таким образом, заменить тригонометрические действия алгебраическими

Для перехода от тригонометрических обозначений к комплексным числам заметим следующее соотношение, которое очевидно из фиг. О 6.

Если ток дан в виде

/ = /;яС08(о)-[-ср),

то комплексное его выражение будет

причем (фиг. 0.6)

Поэтому

а = /т cos {(ut -f ср), =b/mSin (ш+ср).

i=Im [cos {(ut -f ср) -f у sin {mt + cp)].

(0.9)

§ 5. Символическое изображение синусоидальных функций при помощи мнимой степени.

Как известно,

cos6-f ysine = ei). (0.10)

Поэтому взамен выражения

i=7mC0s(a)+cp) (0.14)

мы можем символически писать

/=/ е-м + <р) . (0.15)

Выражения (0.14) и (0,15) отнюдь не тождественны, но второе выражение соответствует первому, поскольку косинусоиде соответствует вращающийся вектор, а вращающемуся вектору соответствует комплексное число.

Оперируя с символическим выражением типа (0.15), мы сильно упрощаем все математические 01[ерации. В любой момент мы можем вновь вернуться к выражению типа (0.14), но при известной привычке к символическому выражению в этом может и не встретиться надобности, так как результаты зачастую могут быть непосредственно поняты из символического выражения в форме мнимой степени или в форме комплексного числа.

Так как

ААт (0.16)

соответствует, как уже сказано, вектору А, имеющему амплитуду Am и составляющему с осью абсцисс угол 6, то при

выражение, полученное после подстановки этих величин в ур-ние (0.16), т. е.

Л = еД ,

соответствует вектору единичной длины, повернутому на угол 90°. Поэтому

= J.

Также легко сообразить, что

е> = 1,

е2 == 1.

Синус и косинус могут быть выражены рядами:

6 О* 6в Также е-* может быу выражено рядом

Если положить

х= уб

[ение е

cos 8-f у sin 6 =

и подставить это в ряд, выражающий значение е*, то из ур-ний (0.11), (0,12) и (0.13) получим тождество

§ 6. Экспоненциальные функции.

Выражение

Д = Ле (0.17)

показывает, что величина А непрерывно возрастает от некоторого начального значения Aq, которое получается при? = 0 так как el). Кривая, соответствующая ур-нию (0.17), показана на фиг. 0.7 и носит название возрастающей экспоненты .

Если А задано в виде функции

- Qt - 1

(0.18)

то кривая получает вид, показанный на фиг, 0.8, и носит название падающей или убывающей экспоненты .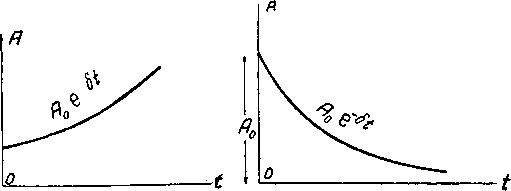

Фиг. 0-7.

Фиг. 0.8.

В обоих случаях закон изменения величины А называется экспоненциальным законом .

Прологарифмировав ур-ние (0.17) или (0.18), получим

In Л = In Ло + что можно представить в виде

In = + S.

(0.19)

(0.20)

Ур-ние (0.20) показывает, что экспоненциальный закон отличается тем свойством, что логарифм отношения величины А в момент времени t к ее начальному значению пропорционален промежутку времени t,

Коэфициент 8 носит название коэфициента возрастания или коэфи-циента затухания (в зависимости от того, стоит ли перед произведением Ы знак плюс или знак минус).

Экспоненциальный, закон соответствует убыванию амплитуды при свободных колебаниях линейных систем. Например, амплитуда колебаний свободного маятника, которые постепенно затухают вследствие трения, убывает по экспоненциальному закону.

По этому же закону Затухают и элек-трические колебания в линейных цепях.

Ток (кли напряжение) в этом случае выражается следующим образом

или символически

i = Im sin (Ы -f- ср) е-

(0.21) (0.22)