на конце линии чисто омическое сопротивление, равное волновому сопротивлению линии.

Физически, как уже говорилось, этот случай означает следующее: вся энергия, доставленная к нагрузке, поглощается здесь, так как и ток и напряжение в нагрузке имеют такую же величину, как и в линии. Движение энергии происходит в одном направлении - от источника к нагрузке.

При бегущей волне значения тока и напряжения в любой точке линии будут:

1х=1то е +

Ёх=1то [/

(2.50)

!?де X-расстояние данной точки от нагрузки (а не от источника).

Линия, в которой существует только бегущая волна, является для источника эдс чисто омической нагрузкой, сопротивление которой равно

В установившемся режиме длина линии играет роль только в отношении сдвига фазы между эдс источника и эдс на концах сопротивления

Если в этом смысле сравнить две точки линии, находящиеся на расстоянии rf, то найдем, что фаза точки, лежащей ближе к нагрузке, запаздывает на угол

Of =z т {х-\- d) - тх = md - -г- d =

(2.51)

Поэтому, если расстояние между источником и нагрузкой равно D, то фаза в нагрузке запаздывает по сравнению с фазой источника

(2.52)

Написанное выражение для угла сдвига от расстояния очень часто встречается и его следует заметить.

§ 10. Случай, когда линия короткозамкнута на конце.

Положим, что конец линии короткозамкнут. Тогда Ет = О и основные ур-ния (2.44) и(2.45) дают:

1х - /то Ёх = /тоР

п + о

П - О

(2.53) (2.54)

Эти выражения показывают, что теперь в проводе существуют прямая и отраженная волны тока и напряжения. Волна тока при отражении не меняет своей фазы (так как знак ее тот же, что и знак прямой волны). Отраженная же волна напряжения меняет знак, т. е. сдвигается по фазе на угол It.

Чтобы выяснить распределение тока и напряжения вдоль провода, перепишем ур-ния (2.53) и (2.54) в тригонометрической форме:

h Ex-

Imo е COS (шх), /We/* sin (шх).

Заменив в ур-нии (2.56) / на е , получим:

/;c=/moe* cos(mx),

Ёх = /mope* +Tsin (шх).

(2.55) (2.56)

(2.57) (2.58)

Исследуем сначала, как распределяются I и Е вдоль линии в один и тот же момент времени. Для этого надо положить t постоянным и рассматривать постоянный для данного значения t множитель /mofr* как

амплитуду. Удобнее всего положить (at или -\- равным нулю. Тогда

fx - IniQ cos (шх), Ёх = /тоР sin (шх).

(2.59) (2.60)

Отсюда видно, что в каждый данный момент ток и напряжение изменяются вдоль линии синусоидально.

При тех значениях, при которых 1х достигает максимума, Ёх равно нулю, и наоборот.

Точки, в которых 1х и Ёх достигают максимальных значений, называются, как уже говорилось, пучностями тока и напряжения . Точки, в которых h и Ёх равны нулю, назьшаются узлами тока и напряжения .

В пучности тока cos(шx)=Г, ав пучности напряжения sin(шx)=l.

Первому условию удовлетворяют точки

шх = 0, 27Г, у тс и т. д.; а так как

ТО эти точки будут находиться на расстояниях

О, т,

2 л . . . 2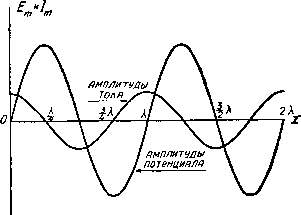

ОТ короткого замыкания. В этих точках будет пучность тока и узел напряжения.

Наобброт, в точках, отстоящих от нагрузки на расстояние

Фиг. 2.7. Отрицательные значения обозначают поворот фазы на 180 .

Т

будет находиться пучность напряжения и узел тока.

На фиг. 2.7 показано распределение амплитуд тока и потенциала вдоль линии, короткозамкнутой на конце при различной ее длине.

Это явление в целом носит название стоячих волн в проводе .

§ 11. Случай, когда линия разомкнута на конце.

Если линия разомкнута на конце, то /0 = 0. Основные ур-ния (2.44) и 2.45)

/. = /

Ех == Ето

П -f О

П + О

получают вид:

1х =

Р L П -О

П -О

Ех = Е,

Р L 2 J

(2.61) (2.62)

Сравнивая их с уравнениями для короткого замыкания (2.53) и (2.54):

П + 0

/дс = /то Ех = /то

п -о

мы видим, что обе системы ур-ний совершенно идентичны. Ур-ния (2.61)

и (2.62) могут быть получены из ур-ний (2.53) и (2.54), если

взамен / написать Е, взамен

Е написать / и взамен р на-

писать -. Р

Поэтому нет надобности вновь подробно анализировать ур-ния (2.61) й (2.62). Очевидно, что мы имеем здесь чистую стоячую волну с пучностью напряжения на разомкнутом конце и на расстояниях, кратных полуволне от этого конца. Первая от разомкнутого конца пучность тока находится на расстоянии четверти волны, а дальнейшие- на расстоянии полуволны друг от друга. На расстоянии четверти волны от пучностей располагаются узлы тока и напряжения. На фиг. 2.8 показано распределение амплитуд тока и напряжения при различной длине линии.

§ 12. Случай, когда линия замкнута на активное сопротивление, не равное волновому.

Если линия нагружена на сопротивление, не равное Болновому, то в ней существуют как стоячие, так и бегущая волны. Бегущая волна доставляет к сопротивлению ту мощность, которая в нем поглощается. Она, как говорят, транспортирует мощность. Стоячие волны появляются потому, что мощность которую способна пропустить линия при дацном напряжещии, больше той, которая может при том же напряжении быть поглощена в сопротивлении. Поэтому часть энергии должна отразиться обратно.

Фиг. 2,8. Отрицательные значения обозначают поворот фазы на 180.