§ 21. Замечание о катушках самоиндукции.

Каждый участок провода обладает свойством самоиндукции, поскольку ток создает вокруг него магнитное поле. При высокой частоте даже небольшие значения коэфициента самоиндукдии L приводят к большому индуктивному сопротивлению /(oL. Поэтому в радиотехнических устройствах и схемах часто приходится считаться с самоиндукцией соединительных приводов, хотя бы они и имели небольшую длину.

При равной длине проводов коэфициент самоиндукции больше у провода, имеющего меньший диаметр. В этом легко убедиться, если сравнить магнитный поток более тонкого трубчатого провода А (фиг. 1.55) с магнитным потоком более толстого трубчатого провода В (фиг. 1.56), в предположении, что по ним идет один и тот же ток. В разрезе, перпендикулярном оси провода, магнитные линии представятся кольцами.

Поток А включает такие же кольца, как В, но, кроме того, еще ряд колец, диаметр которых меньше диаметра В. В случае сплошных проводов.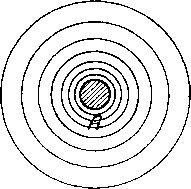

Фиг. 1-55.

Фиг. 1.56.

дело обстоит так же, потому что, как будет сказано ниже, высокочастотный ток идет по поверхности проводника и не проникает сколько-нибудь-значительно внутрь его.

По этой причине для осуществления самоиндукции следовало бы применять тонкие провода, а для уменьшения индуктивного сопротивления проводки следует применять толстые провода.

Это, однако, не всегда оказывается возможным. В мощных установках тонкие провода, обладающие малой поверхностью, будут в состоянии отводить выделяющееся в них тепло только при очень высокой температуре и могут сгореть. Поэтому здесь приходится итти на значительное увеличение диаметра, а следовательно, и длины провода, чтобы получить надлежащую самоиндукцию.

Толстые соединительные провода обладают другим недостатком - они создают большую емкость.

В приемных цепях самоиндукции могут осуществляться из очень тонких проводов. Количество выделяющегося тепла здесь ничтожно, а увеличения потерь вследствие уменьшения диаметра бояться не следует, так как вместе с уменьшением диаметра (для получения одного и того же коэфициента самоиндукции) уменьшается длина провода.

Наивыгоднейшей формой замкнутого провода (с точки зрения получения наибольшего коэфициента самоиндукции при той же длине провода) является один круговой виток.

Однако, если требуется получить большой коэфициент самоиндукции, диаметр витка окажется слишком большим. Поэтому прибегают к сворачиванию проволоки во многовитковые катушки или спирали.

Длина провода в таких катушках больше, чем длина провода ,в одном круговом витке при том же коэфициенте самоиндукции.

Наивыгоднейшим сечением катушки является круглое.

Если предположить, что витки катушки расположены в идеальной близости один к другому так, что магнитный поток каждого витка пронизывает все остальные витки, то коэфициент самоиндукции окажется пропорциональным квадрату числа витков. Действительно, если бы одинаковые витки находились далеко один от другого и не оказывали бы друг на друга никакого влияния, полная эдс самоиндукции оказалась бы равной сумме всех эдс, т. е. была бы пропорциональна числу витков. Но в рассматриваемом идеальном случае в каждом витке от всех остальных витков наводится еще эдс вследствие взаимного влияния (взаимная индукция). Поэтому, если число витков п и собственная самоиндукция каждого витка Lg, то эдс на концах каждого витка ЬдП, а на концах всей катушки пЬаП = ЬдП.

Этот коэфициент самоиндукции следовало бы назвать действующим коэфициентом самоиндукции , но обычно слово действующий опускают.

Его можно было бы вычислять по формуле

L = . (1.113)

В действительности весь магнитный поток одного витка не пересекает все остальные витки. Каждый виток получает от остальных только часть потока, вообще тем меньшую, чем он дальше от него расположен. Кроме того витки могут лежать не все в одной плоскости. Поэтому в действительности коэфициент самоиндукции

И может быть выражен формулой

L = K-, (1.115)

где к-некоторый множитель, зависящий от формы и размеров провода и конструкции катушки.

Точное вычисление самоиндукции представляет собой сложную задачу даже для одного кругового витка. Точное же вычисление самоиндукции катушки часто оказывается невозможным. Поэтому довольствуются приближенными полуэмпирическими формулами, некоторые из которых приведены в приложениях II и III.

§ 22. Емкость катушек.

Положим, что к концам катушки приложена извне синусоидальная разность потенциалов. Эта разность потенциалов, распределенная между витками катушки, и обусловливает появление электрического поля в пространстве между ними.

Каждая соседняя пара витков может рассматриваться как конденсатор некоторой емкости С. Мекду этими витками образуется электрическое поле.

Вся катушка может быть эквивалентно заменена схемой фиг. 1.57. Самоиндукция, приходящаяся на один W виток, различна в различных частях катушки. А именно, витки, лежащие в центре катушки, имеют большее L вследствие бол.ее сильного воздействия на них взаимной Фиг. 1.57. индукции от остальных витков. Витки, лежащие ближе

к краю катушки, имеют относительно меньшее значение L. Если принять, что ток / одинаков по всей длине катушки, то падение потенциала, приходящееся на один виток, больше, следовательно, в середине катушки и меньше у ее краев.

Поэтому в середине катушки запасается больше электричества в виде зарядов, чем у ее краев.

В первом приблизении катушка может рассматриваться как комбинация из параллельно включенной емкости Сд: и самоиндукции 1 (фиг. 1.58).

Эквивалентное сопротивление г на фиг. 1.58 замещает диэлектрические потери в изоляции провода и каркасе, на который намотана кадушка. Эти потери при высокой частоте могут быть значительны. Обычно стремятся придать обмотке такую конструкцикь

чтобы отношение

было максимально.

Фиг. 1.58.

в этом смысле особенно невыгодными являются двуслойные катушки, намотанные обычным образом.

Начальные витки первого ряда Л (фиг. 1.59) и последние витки второго ряда В находятся на одном конце катушки в непосредственной близости друг к другу. Они образуют конденсатор, запасающий большое количество электричества вследствие того, что разность потенциалов здесь максимальна.

С целью уменьшения емкости в двуслойных катушках прибегают к такому способу цамотки, при котором первый виток второго слоя кладется непосредственно на первый виток первого слоя. После этого кладется второй виток первого слоя и на него второй виток второго слоя и т. д. Этим избегается накопление больших разностей потенциалов между близлежащими витками.

Далее применяются различные виды намоток, при которых провода двух соседних витков располагаются не параллельно друг другу. Так например, на фиг. 1.60 показана схема двух рядов проволоки при так называемой корзиночной намотке. Каждый ряд представляет собой многоугольник.

Второй ряд повернут относительно первого на некоторый угол. Следующий ряд той же формы поворачивается еще на некоторый угол. Таким образом провода удаляются друг от друга.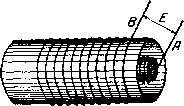

Фиг. 1.59.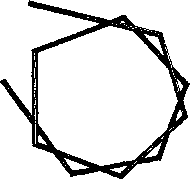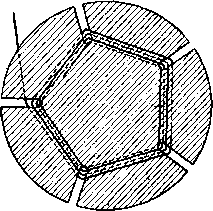

Фиг. 1.60.

Фиг. 1.61.

Вторая распространенная разновидность катушек этого рода - это так называемая плоская корзиночная катушка.

Способ ее намотки показан на фиг. 1.61. Основанием обмотки служит пресшпановый круг, на который спирально намотан провод, удерживаемый в радиальных прорезах. Число прорезов должно быть нечетным.