Оно может быть также дано в виде некоторой кривой, как например кривая фиг. 0.2.

Чтобы изучить встречающееся в радиотехнике бесчисленное количе-ство всевозможных видов F{t) (или бесчисленное количество форм кривых, выражающих эти функции), все их можно свести к некоторому, относительно небольшому, числу типов, обладающих определенными признаками и свойствами. На протяжении курса мы будем неоднократно отмечать такие характерные типы кривых.

Этот способ представляется во многих случаях очень удобным и важным, так как дает возможность предвидеть хара1<тер явлений в электриче-CKHjc цепях, в которых действует данная эдс или данный ток, и оценивать эти явления с их качественной стороны.

Однако гораздо более общим (и притом дающим возможность количественной оценки) является такой способ представления, при котором данная сложная функция рассматривается как сумма или шк произведение некоторых более простых функций, действие которых на данную цепь хорошо известно. В случае линейной системы действие данной сложной функции будет равно сумме действий элементарных функций, на которые она разложена.

Очевидно, что этот способ получит универсальное значение в том случае, если все возможные виды функций будут приводиться к сумме или к произведению одних и тех же элементарных функций, если эти последние окажутся удонЬщи для математического анализа и, наконец, если действие их на электрические цепи может быть удобно изучено.

В этом смысле практически наиболее удобными оказываются синусоидальные и экспоненциальные функции. Синусоидальные функции (соответствующие гармоническим колебаниям) позволяют выразить всякую функцию имеющую интерес для радиотехники, в виде ряда или интеграла Фурье. Произведение синусоидальной функции на экспоненциальную дает возможность простейшим образом выразить гармоническое колебание, амплитуда которого постепенно уменьшается со временем вследствие расхода энергии в цепи.

Наконец, в более сложных случаях и, в частности, при изучении явлений в длинной проволочной линии, когда на величину эдс или тока влияет не только координата времени, но и координата пространства, удобно пользоваться гиперболическими функциями.

Все эти три вида функций, как это будет показано ниже, весьма родственны между собой и могут быть приведены к экспоненциальной функции с комплексным показателем, на которой ниже мы поэтому подробно остановимся.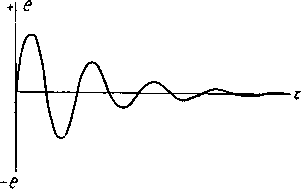

Фиг. 0 2.

§ 4. Символическое изображение синусоидальной функции комплексным числом.

Если синусоидальная функция записана в виде

i = lm Sin(o)/-f ср),

(0.3>

то математически это означает, что переменный ток / продолжается от / = - сю до t--\-oo, т. е. всегда.

На самом деле всякий переменный ток, наблюдаемый на опыте, продолжается в течение некоторого ограниченного времени и должен быть записан так:

r=s/ sm((fl-f <р)прих1>/<т2 I

i = О при всех остальных значениях / J

(0.4)

Кривая, изобажаюдцая ток, длящийся от f = % до не ехть уже

синусоида в математическом смысле, и мы должны называть ее отрезком синусоиды .

Очевидно, что если бы существовал ток, выражаемый ур-нием (0.3), то для того, чтобы убедиться, что мы имеем дело с действительной синусоидой, а не с отрезком синусоиды, потребовалось бы бесконечное время. Так как время, имеющееся в нашем распоряжении, всегда ограничено, то нельзя путем физического опыта отличить действительную синусоиду от отрезка синусоиды, длящегося дольше, чем время опыта.

Из этого следует, что если отрезок синусоиды длится дольше того времени, в течение которого исследуется действие тока или напряжения

на наши приборы, и если за это время все явления приобретут установившийся характер, , то математически мы-с полным правом можем пользо-\ ваться выражением (0.3). В противном

/ Jh> случае надо пользоваться выраже-

нием (0.4).

Для математических операций тригонометрическое выражение (0.4)

не всегда оказывается удобным, так

----* 1 как действия с тригонометрическими

ffcos(e) I функциями приводят к громоздким

/ вычислениям. Часто гораздо удобнее

/ пользоваться так называемым сиМво-

/ лическим методом, сущность кото-

рого мы вкратце напомним, . Возьмем в прямоугольной коор-

динатной системе (фиг. 0.3) отрезок А, который будем считать вектором, Фиг. 0.3. т. е. припишем ему, кроме длины А,

еще и направление, указанное стрелкой. Пусть это направление составляет угол 6 с осью абсцисс.

Будем удерживать начало этого вектора в начале координат, а конец его заставим двигаться по окружности с равномерной угловой скоростью О). Тогда

6 = 0) + 9, (0.5)

причем ср зависит от выбора момента начала отсчета времени t.

Положим, что длина вектора численно равИа 1т- Тогда проекция вектора на ось абсцисс будет

i = 1т cos (lot--f), (0.6)

т. е. будет выражать собой гармоническую функцию.

Обратно: каждой гармонической функции соответствует, следовательно, некоторый вращающийся вектор. Длина этого вектора равна амплитуде, а угол с осью абсцисс - фазе гармонической функции. Следует обратить внимание на то, что гармоническая функция при этом вовсе не отождествляется с вращающимся вектором, а устанавливается лишь соответствие между ними. Это соответствие, однако, таково, что каждой гармонической функции соответствует только один вектор. Это позволяет заменить действия

С тригонометрическими величинами действиями с соответствующими им векторами. Вместо того, чтобы склад1з18ать, вычитать, делить или перемножать тригонометрические Гфункций эти действия можно производить с соответствующими! им векторами. Результирующий вектор будет соответствовать результирующей тригойолгетрическоЙ функции.

На первый взгляд может показаться, что подобная операция только усложняет дело, так как вводится некоторое новое понятие, которое требует освоения. В действительности это не так. Операции с векторами оказываются значительно проще, если для их изображения применить комплексные числа-

Очевидно, что вектор А (фиг. 0.4) может быть представлен как сумма вектора а и перпендикулярного ему вектора Ь.

Если условиться выражать расстояния от начала координат вдоль оси Х-ов действительными числами, то вектор а вполне определится одним единственным числом, выражающим его длину. Направлению вправо от начала координат будет соответствовать знак -}- , а влево -знак ~

Второй составляющий вектор, изобража-емый отрезком Ь, уже не можег быть просто определен числом, так* как он отличается от первого вектора еще и направлением.

Это изменение направления можно было бы отметить каким-нибудь условным знаком, который позволил бы не спутать вектора одного направления с векторами другого.

В этом случае и второй вектор можно было бы также обозначать числом с указанным значком, причем число и знак опять-таки выражали бы длину вектора и направление его вверх лио вниз.

Можно поступить и иначе. Заметив, что умножение числа, выражающего длину вектора, на (- 1) поворачивает направление вектора на 180, посмотрим, нельзя ли найти такое число, умножение на которое поворачивает вектор на x0°. Обозначим это число буквой /. Так как двойной поворот вектора на 90 создает поворот на 180°, то очевидно, что двойное умножение числа на / должно дать (-1).

Поэтому

или

У = У=Т)-

1) Совершенно так же, например, повороту на 45° будет соответствовать умножение числа, выражающего длину вектора, на число

Равным образом умножение, например, на число

соответствует повороту на 10°. Выражение

соответствует вектору длиной А, повернутому относительно оси абсцисс на угол в. Выражение

оответствует вектору, вращающемуся с частотой ш.

В обоих последних случаях вектор выражен уже не комплексным числом, а степенно функцией.

С аналогичным изображением вектора, но в другой форме, мы встретимся дальше.