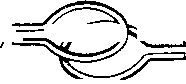Величина носит, как известно, йазвание индуктивного сопротивления . Если L выражено в генри, то <oL получается в омах.

Для сокращения речи величину L называют просто самоиндукцией опуская слово коэфициент .

В своем прямом смысле термин самоиндукция относится к приборам, которые предназначены в электрических цепях играть роль индуктивного сопротивления.

§ 19. Взаимная индукция.

Действие одной электрической цепи на другую или одной части цепи на другую часть может быть обусловлено магнитным полем, индуктирующим эдс.

В этом случае говорят, что две цепи Я. * / части связаны магнитной связью. - Рассмотрим магнитную связь двуз(

катушек. Положим, что по витку а, (фиг. 1.50) идет переменный ток i, образующий JJJYTso. магнитный поток Ф. Часть силовых линий

этого потока, которую обозначим Фг, входит в другой виток fla и возбуждает в нем эдс

. = -. (1-86>

Поток Фз пропорционален току zj и зависит от взаимного расположения и размеров обеих катушек. Обозначим

Р = М (1.87)

и назовем М- коэфициентом взаимной индукции, учитывающим влияние первой катушки на вторую. Тогда

.,= -М,а. (1.88)

Совершенно так же, если по второй катушке идет ток в катушке возбуждается эдс

е,=--М . (1.89)

М = р, (1.90)

Т. е. представляет собой коэфициен-т взаимной индукции, учитывающий влияние второй катушки на первую. Можно доказать, что

Ml2 = M2i, (1.91)

и поэтому вместо (1.89) и (1:88) можно написать

(1.92)

Или в случае синусоидального тока

1 = - ]ШК

(1.93)

§ 20. Соединение самоиндукций.

Если две самоиндукции и не связаны одйа с другой магнитной связью, общий коэфициент самоиндукции при последовательном соединении будет равен сумме Li и L, т. е.

т. е.

При параллельном соединении будет

(1.94)

(1.95) (1.96)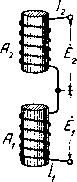

Фиг. 1.51.

Иначе обстоит дело, если, например, две катушки связаны магнитной связью.

В этом случае в каждой катушке, кроме эдС от собственной самоиндукции, возникает еще эдс, наведенная вследствие взаимной индукции другой катушкой.

Рассмотрим два простейших случая. Катушки и (фиг. 1.51), лишенные омического сопротивления, соединены последовательно. Витки их направлены в одну сторону и магнитные поля их взаимно усиливаются.

В этом случае ток /j равен току /2.

Напишем уравнения, определяющие эдс на концах первой катушки и эдс Eg - на концах Второй катушки:

£1-/ш(£Л + мД)

О, О,

1 + 2

/w(Li + 2 + 2М)

(1.97) (1.98) (1.99)

(1.100)

Так как в числителе стоит полная эдс на концах всей цепи, то в знаменателе стоит сопротивление всей цепи. Поэтому величина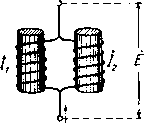

L==Li-f L2 + 2M

(1.101)

играет роль самоиндукции обеих катушек, соединенных последовательно при одинаковом направлении витков. При противоположном направлении витков в одной из катушек или при противоположном соединении катушек получим

L = Li + L2 -2М.

(1.102)

Фиг. 1.52.

Можно соединить катушки параллельно. Если при этом магнитные поля катушек взаимно усиливаются (фиг. 1.52), то уравнения напишутся так:

-/ш (£Л + М/,) = 0, -/ш (£Л + М)=0,

(1.103) (1.104) (1.105) 61

Решая эти уравнения, получим

(1.106)

После упрощения знаменателя эта формула будет иметь вид

/1 + 4 =

(1.107)

Выражение, стоящее в знаменателе множителем при /со, играет роль коэфициента самоиндукции. Если М = 0, то

В этом случае

Li + L,

Очевидно, что L меньше, чем Lj и чем Lg. Если Li = L2 и М = 0, то

г 2 .

если Lj=Lc, и MLi, то

1 2*

(1.108) (1.109)

(1.10) (1.111)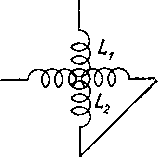

При противоположном направлении витков знак при М изменится на обратный. Тогда при условии М и = получим

LO. (1.112)

В радиотехнике распространены приборы, служащие для получения изменяющейся самоиндукции

путем изменения ко-

Zy эфициента взаимной,

/ индукции. Такие

приборы называются вариометрами. На схемах переменная самоиндукция изображается символом, показанным на фиг. 1.53. Если хотят указать, что катушки в вариометре соединены определенным образом, например последовательно, то применяют графический символ, например, фиг. 1.54.

Изменение М достигается или путем изменения расстояния между катушками, или чаще путем поворота плоскости одной катушки относительно другой.

Если плоскости взаимно перпендикулярны, то магнитная связь отсутствует {к = 0 и М = 0). Если плоскости параллельны, то взаимная индукция достигает некоторой наибольшей в данной конструкции величины. Практически при этом в вариометрах без железного сердечника максимальный

коэфициент связи обычно бывает меньше или, иначе говоря, меньше 50%.

Фиг. 1.53.

Фиг. 1.54.