Например, напряженность поля по величине будет равна единице, если ток равен одной электромагнитной единице (10 а), а расстояние от центра провода равно 2 см.

Нашей главной задачей является выяснение связи между магнитным и электрическим полем. Эта связь лежит в основе всех электрических явлений. Для понимания тех явлений, которые использует радиотехника, она должна быть особенно хорошо усвоена.

§ 16. Связь магнитного поля с электрическим полем.

Связь между электрическими и магнитными явлениями была установлена еще в 1820 г. шведским физиком Эрстедтом, открывшим действие тока на магнитную стрелку.

Но в полной мере эта связь была раскрыта работами английского физика Фарадея, который открыл так называемое явление электромагнитной индукции, т. е. получение электрического поля посредством магнитного.

Величайшей заслугой Фарадея было то, что он первый понял, что электрические и магнитные явления происходят в пространстве, окружающем провода, а в самих проводах происходит только гашение электромагнитной энергии, т. е. превращение ее в тепло.

Другой английский физик Максвелл развил идеи Фарадея, придал им строгую математическую форму и в математической форме формулировал законы, лежащие в основе

электродинамики, т. е. учения об электромагнитных явлениях.

На основании установленных им законов Максвелл теоретически предсказал существование электромагнитных волн, которые позже были открыты Герцем и применение которых создало радиотехнику.

Связь между магнитным и электрическим полем проявляется в следующем.

Всякое движущееся электрическое поле (например поле движущегося заряда) создает магнитное поле. Направление магнитной силы в возникающем таким образом поле перпендикулярно направлению движения и перпендикулярно направлению электрической силы в движущемся поле.

Так например, на фиг. 1.46 тонкими прямыми линиями изображены силовые линии электрического поля. Стрелка со значком v показывает, что это поле движется вправо, причем направление движения перпендикулярно направлению электрической силы. В этом случае возникает магнитное поле

® @

©

® ©

©

® ®

®

ф ©

©

Фиг. 1.46.

Фиг. 1.47.

(1.79)

Здес1? Н - напряженность поля в электромагнитных единицах, е - диэлектрическая проницаемость среды, v -скорость движения, с -скорость света, Е - напряженность электрического поля в электростатических единицах.

Линии магнитного поля перпендикулярны направлению движения и направлению электрической силы.

На фиг. 1.46 магнитные линии или трубки изображены в сечении кружками с точкой внутри. Это обозначает, что линии направлены из-за чертежа к наблюдателю. На фиг. 1.46 электрическая сила направлена вверх, а на фиг. 1.47 -вниз. Соответственно этому магнитные линии изображены кружком с крестиком, что показывает направление их от наблюдателя за чертеж.

Вообще, чтобы определить направление магнитной силы, пользуются правилом буравчика, которое для данного случая применяется следующим образом.

Если Е и Н в точке а изобразить векторами (фиг. 1.48), то направление кратчайшего перехода от конца Е к концу Н совпадет с направлением

вращения рукоятки правовинтового буравчика, ось которого, помещенная в точке а, совпадет с направлением движения положительного заряда. Буравчик при завинчивании перемещается в ту же сторону, куда направлено движение положительного заряда. На фиг. 1.48 направление кратчайшего перехода .от Е к Н изображено стрелкой. Острие буравчика при указанном на фиг. 1.48, расположении Е и Н направлено за чертеж.

Если направление движения не перпендикулярно направлению Е, а составляет с ним угол ср, то поле может быть разложено на две составляющие: перпендикулярную движению и совпадающую с ним. Первая будет Ei = Е sin ср; Фиг. 1.48. ана явится причиной магнитного поля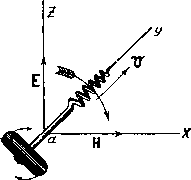

H = -Ei= -Esincp.

(1.80)

Вторая не дает никакого поля, так как движение силовой линии вдоль своей оси неможет привести к изменению энергии поля. Иначе говоря, при этом движении сил инерции не появляется.

Совершенно так же при движении магнитного поля (например при движении магнита) перпендикулярно линиям этого поля и перпендикулярно направлению движения возникает электрическое поле.

Напряженность его определяется равенством

E = lf = В.

(1.81)

Направление Е определяется тем же правилом.

\ \ М \ М 111111/ \\ \ \ \ \ \ \ \ I ;/, i I м I I I ! I 1 1 I / (

! I 11 1; i \ \

. / / / / ; I I i 1 I > > \ \

/ i I I I I I I . > > t у у Ч ч

§ 17. Магнитное поле тока проводимости и тока смещения.

Указанное в § 16 взаимное превращение электрической и магнитной энергии обычно .удобнее выражать в другой форме. Когда мы имеем дело с электрическими цепями, то бывает лроще рассматривать не поля, а соответствующие им токи напряжения, которые мы относим к элементам, составляющим цепь (т. е. к емкостям, самоиндукциям и сопротивлениям).

Например, возьмем цепь постояв- , ного тока, состоящую из элемента Е, проводов и сопротивления R (фиг. 1.49 (.

Явления в такой цепи в действительности заключаются в том, что элемент создает электрическое поле. Линии

этого поля непрерывно движутся по направлению к сопротивлению R вдоль проводов. В сопротивлении R силовые линии и энергия их переходят в тепло. Вследствие движения электрических линий возникает магнитное поле. Таким образом присутствие магнитного и электрического поля является следствием движения энергии по проводам от Е к R.

Пользование этим вполне правильным представлением может затруднить как измерения, так и вычисления.

Фиг. 1.49.

гораздо проще в данном случае пользоваться понятием о напряжеиии элемента и токе в цепи. Обе эти величины легко и удобно измерить.

В этом случае мы говорим, что магнитное поле обусловлено током, и можем вычислить его пЬ соответствующим формулам.

Таким же образом, в случае переменного тока, вместо движения силовых линий часто удобнее рассматривать опять-таки не движение силовых линий, а два тока. Один из этих токов называется током проводимости, т. е. тем самым обыкновенным током, который мы считаем текущим по проводам. Второй ток - это тот тсгк, который протекает в месте разрыва проводниковой цепи, т. е. емкостный ток.

Величина его равна

/=С. (1.82)

Этому току в диэлектрике конденсатора соответствует изменяющийся во времени поток электрических линий. Так, вместо ур-ния (1.82) можно равнозначно написать

. = . (1.83)

Этот ток носит название тока смещения . Поскольку ток проводимости мы относим к проводам, постольку ток смещения мы должны относить к диэлектрику (в котором происходит изменение потока индукции).

Так же, как и ток проводимости, ток смещения образует вокруг себя магнитное поле.

§ 18. Коэфициент самоиндукции

Если по витку проволоки идет переменный ток. то внутри этого витка существует изменяющийся магнитный поток, который создает в витке эдс,

пропорциональную скорости изменения потока, т. е. величине Гак как

поток пропорционален току, то эдс может быть выражена формулой

е--Z.;, (1.84)

где L - некоторый материальный коэфициент, характеризующий данную цепь в смысле соотношения между током и магнитным потоком ).

Этот коэфициент носит название коэфициента самоиндукции .

В случае синусоидальной эдс ур-ние (1.84) перепишется так

E=-/a)L/.2) (1.85)

За единицу коэфициента самоиндукции принимается самоиндукция такого провода, в котором при равномерном изменении тока на одну единицу в секунду наводится единичная эдс.

В практической системе (ампер-вольт) единица L называется генри*. В абсолютной электромагнитной системе эта единица называется сантиметр

1 гн= 10 см.

В радиотехнике часто приходится иметь дело с малыми самоиндукциями, и поэтому выражение L в сантиметрах очень употребительно.

) Так же, как емкость характеризует даннук цепь в смысле соотношения между напряжением и потоком электрической индукции.

2) Если i = Ijfi е , ТО- / = п/сое Таким образом символ А при комплексном изоб-dlt dt

ражении величин заменяется множителем / л. При этом о вообще может быть комплексной величиной.