каверн, наполненных газом. В последнем случае сначала наступает ионизация и пробой газа, следствием чего в дальнейшем является разрушение твердого диэлектрика.

Поэтому пробивное напряжение, даже в однородном поле, вообще, зависит от длительности действия напряжения.

При высоких частотах разрушение твердого диэлектрика чаще наступает вследствие большого количества выделяемого тепла, которое, как мы увидим ниже, растет с частотой.

Пробой газовых диэлектриков при высокой частоте облегчается более благоприятными условиями ионизации газа,

§ 10. Потери в диэлектриках.

Среди всех других явлений в диэлектриках для техники большой частоты особенно большое значение имеют явления, приводящие к потере энергии.

Каким бы внутренним механизмом в диэлектрике ни были вызваны эти потери, они формально могут быть эквивалентно заменены действием некоторого омического сопро- О

тивления, включенного параллельно или последовательно с конденсатором.

Такая замена облегчает изучение и взаимное сравнение различных диэлектриков й позволяет легко вычислить количество энергии, выделякщейся в конденсаторах под действием высокой частоты, л

В случае замены данного конденсатора дей-ствием параллельного сопротивления эквивалентная схема получит вид фиг, 1,25,

Рассмотрим, каково сопротивление такой цепи для напряжения, приложенного в точках Л и В,

Чтобы найти Z, поступим следующим образом. Сначала найдем проводимость между точками А и В, Она равна

- = + /*. (1-51)

Фиг. 1,25.

Причем

а = - г

-/шС

1 2 г

(1.52)

(1.53)

Можно было бы рассуждать иначе, а именно, предположить, что вся система представляет собой некоторую емкость Cj, так что

/ = /EcdCi.

В этом случае емкость надо было бы считать комплексной

Ci = C-/C2,. Из ур-ний (1.54) и (1.55) получим

/ = /о) (С - /Со) к = (шСз -f ушС) Е

-1-=:ш(С2 + /С).

(1.54) (1.55)

(1.56)

(1.57) 45

при диэлектрике с проводимостью вводят понятие о комплексной диэлектрической проницаемости, применение которой в некоторых случаях оказывается очень удобным.

Действительно, емкость может быть выражена произведением

С = Ле, (1.58)

где А некоторое число, зависящее исключительно от геометрии поля.

Аналогично этому комплексная емкость может быть выражена через, произведение

Ci = Aeo, (1.5Я>

где - комплексная диэлектрическая проницаемость. Вернемся снова и ур-нисю (1.51).

Обозначим угол сдвига между емкостным током и полным током череа

g jz

тогда

tg8 = -f. (1.60)

Для нас далее будет интересен случай, когда а<Ь. Для этого случая можно положить

tg8 = -f0 (1.61)

tg8 = = 8. (1.62 >

мощность, выделяемая в сопротивлении г, выразится следующим образом

Р = -. (1.63)

Подставив значение- из ур-ния (1.62), получим

РшС8Е2 при 8<С: 1. (1-64)

Из этого выражения видно, что потери в утечке (при условии, что ее проводимость мала по сравнению с емкостной проводимостью) пропорциональны углу 6. Этот угол носит название угла потерь .

На фиг. 1.26 показан способ соединения, при котором емкость и сопротивление включены последовательно. Полное )Сопротивление в этом случае будет

Z=ff-4 (1.65)

В этом случае также можно говорить о комплексной проводимости всей системы, равной или ввести понятие о комплексной емкости.

Легко получить для выражения ~а-{-jbi значения

Угол потерь

(1.68)

Мощность, выделяемая в сопротивлении.

при S< 1

(1.69) (1.70)

Угол потерь является чрезвычайно удобной характеристикой диэлектрика или конденсатора в целом и легко находится экспериментально.

Из ур-ний (1.62) и (1.68) получим для двух рассмотренных эквивалентных схем

tg8 = ;; или tgb==<aCR,

другими словами, если потери в диэлектрике таковй, что угол потерь уменьшается пропорционально частоте, то они могут быть эквивалентно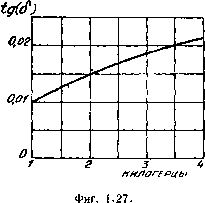

Фиг. 1.28.

замерены омической утечкой. Потери этого рода могут быть обусловлены, например, сквозным током, идущим ерез конденсатор.

Если угол потерь возрастает пропорционально частоте, то потери могут быть эквивалентно заменены действием последовательного сопротивления.

Имея кривые tg8 = /(a)), можно в известной мере ориентироваться на основании этих соотношений в характере потерь в данном диэлектрике.

Так например, на фиг. 1.27 показано изменение tgS в зависимости от частоты для парафинированной бумаги при температуре 15°Ц, Угол потерь пропорционален частоте и, следовательно, потери носят характер последовательно включенного сопротивления. Как мы увидим ниже, это соответствует потерям на внутреннее трение в диэлектрике.

На фиц. 1.28 дана кривая для того же конденсатора при температуре-80°С. Падающий характер кривой указывает, что преобладают потери, имеющие характер омической утечки.