Отсюда емкость

(1.20)

Если дать Га значение оо, т. е. предположить, что силовые линии заканчиваются на весьма удаленных проводниках, то

С = £Г1. (1.21)

Таким образом емкость уединенного шара численно равна его радиусу. Второй способ основан на вычислении потенциала. Мы применим его для вычисления емкости между двумя шарами, находящимися на большом

расстоянии от всех остальных предметов. Диаметр шаров предположим малым по сравнению с расстоянием между ними. Это последнее позволит считать, что заряды на поверхности шаров распределены равномерно (т. е. заряды одного шара не смещены под влиянием зарядов другого шара).

Сообщим шару А (фиг. 1.8) заряд+Q, а шару В заряд -Q.

Потенциал у поверхности шара В составится из двух слагаемых. Во-первых, собственный заряд шара В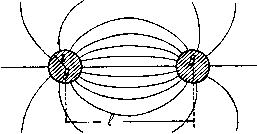

Фиг. 1.8.

дает на его поверхности согласно ур-нию (1.9) потенциал (при е=1)

1=-Я (1.22)

где г - радиус шара.

Во-вторых, заряд шара А создает в центре шара В потенциал

(1.23)

где / - расстояние между шарами.

При условии, что расстояние I велико по сравнению с радиусом шара В, можно принять, что / есть расстояние от А до любой точ1и поверхности шара В.

Тогда ур-ние (1.23) даст потенциал, наводимый на поверхности шара В зарядом шара А.

Следовательно, полный потендиал шара В будет

Совершенно так же найдем, что полный потенциал шара А будет

rj Q Q

(1.24)

(1.25)

Вычитая один потенциал из другого, получим разность потенциалов между шарами, которую теперь обозначим Е

Отсюда емкость между шарами

Е 2

(1.26)

(1.27)

Если шары помещены не в воздухе, а в среде с диэлектрической проницаемостью е, то получим -

(1.28)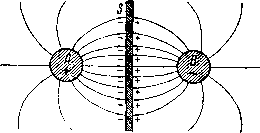

Фиг. 1.9.

Разумеется, этот результат применим для практики только при определенных условиях. Если г будет сравнимо с /, то заряды на каждом из шаров заметно перераспределятся под влиянием поля другого шара. Вследствие этого большее количества электричества соберется на той стороне поверхности каждого шара, которая обращена к другому шару. Собственное поле Л и В не будет уже радиальным. Емкость окажется больше, чем вычисленная.

Если / будет слишком велико, то шары нельзя будет в реальной обстановке рассматривать как уединенные от-всех других предметов. Все эти предметы наведут свои потен-1;иалы или, иначе говоря, изменят конфигурацию поля. Вследствие этого взаимная емкость обычно станет меньше вычисленной.

В случае двух одинаковых шаров, заряженных до равных, но противоположных потенциалов, картина поля получается совершенно симметричной. Поэтому в середине между шарами вдоль плоскости, перпендикулярной к линии, соединяющей их центры, потенциал равен нулю. Если поместить здесь, как показано на фиг. 1.9, проводящую тонкую и очень обширную пластину, имеющую нулевой потенциал, то форма поля во всем пространстве не изменится. Однако у самой пластины силовые линии разорвутся и образуются отрицательные заряды на стороне шара А и положительные на стороне шара В.

Мы можем теперь уничтожить поле со стороны шара А, например, приблизив шар А до соприкосновения с плоскостью S. Поле со стороны шара В останется неизменным.

Разность потенциалов между 5иВ равна половине разности потенциалов между AvlB. Количество электричества осталось тоже. Воспользовавшись ур-нием (1.28), найдем, что емкость между плоскостью S и шаром В равна

С = -. (1.29)

Часто при вычислении емкости бывает удобно поступить обратно, заменяя проводящую плоскость воображаемым зеркальным изображением данного заряженного предмета.

Например, емкость, приходящаяся на единицу длины двухпроводной линии, определяется фор-

- (1.30)

Фиг. 1.10.

4 In

где / - расстояние между центрами проводов, а г - радиус провода.

Положим теперь, что мы имеем однопроводную линию, подвешенную на высоте h над землей. Действие проводящей поверхности земли заменяют зеркальным изображением провода. Картина, которая получится в разрезе перпендикулярно оси провода, показана на фиг. 1.10. Здесь 55 -поэерх-

ность земли; Л -сечение провода; В -сечение его зеркального изображения; / = 2Л - расстояние между А и В. Пользуясь ур-нием 1.30, пишем

= = (1.31)

4 In -i- 4 In -г г

Для воздушной линии е=1.

§ 5. Единицы измерения емкости.

Все предыдущие формулы написаны в электростатических единицах. Электростатическая CGS единица емкости, называемая сантиметром, удобна для измерения небольших емкостей, и в радиотехнике ею постоянно пользуются. Практическая единица - фарада равна 9-10 см.

Электростатическая CGS единица напряжения (разности потенциалов),

равная 300 в, и единица количества электричества, равнаят к, на практике не применяются, но при теоретических выводах ими приходится пользоваться из соображений однородности величин.

При - пользовании формулами необходимо, как известно, пользоваться однородными единицами. Для перевода найденных выше формул в практическую систему следует взамен С писать Сд-ф, взамен Я писать Я 300 в,

взамен Q писать Q /д к и взамен мощности Р писать Р . 10в/л.

Если формулы содержат только электрические величины, для которых на практике всегда применяются только практические единицы, то формулы остаются неизменными. Например, Q = EC; Е 300 в С --j ф =

= ТЛО или EC = Q.

Преобразование необходимо только в случае наличия неэлектрических величин, например длины.

Например, емкость между двумя параллельными плоскостями при равномерном поле в электростатических единицах была найдена

с = if, см. (1.32)

В практической системе

=410 (1-33)

причем длина d и площадь 5 выражены в сантиметрах и квадратных сантиметрах.

§ 6. Основные формы конденсаторов и вычисление их емкости.

Прибор, назначением которого является создание емкости, как известно, называется конденсатором.

Конденсаторы, применяемые в радиотехнике, чрезвычайно разнообразны по своему устройству и назначению.

Они строятся как для получения постоянной емкости, так и для емкости, изменяющейся в некоторых пределах.

Так как при высоких частотах даже очень маленькие емкости могут образовать довольно значительную емкостную проводимость, то в отличие от техники сильных токов в радиотехнике находят себе применение конденсаторы емкостью от нескольких сантиметров до нескольких десятков микрофарад. Очень большое значение получают здесь различного рода так называемые паразитные емкости, т. е. емкости, образуемые подводящими ороводами и различными элементами приборов и схем, что также не имеет места в технике сильных токов.