На расстоянии dr

dA = Fdr = + . 1. dr. (1.6)

Если заряд Qi переходит с расстояния г на расстояние г , то работа будет

A±f<lr±(l-). (1.7,

Положив К = оо (т. е. считая, что заряд приведен в данную точку из бесконечности) и Qi = l, получим

А = ±5-. (1.8)

Эта работа, совершаемая единичным зарядом при проведении его из бесконечности, называется потенциалом данной точки поля. Очевидно, что а) при передвижении заряда по сфере, в центре которой помещен заряд Q, работа не затрачивается; б) работа не зависит от того, по какому пути заряд был проведен в данную точку; в) работа, совершаемая зарядом при передвижении по любому замкнутому пути, равна нулю.

В случае точечного заряда поверхность сферы является поверхностью равного потенциала.

Величина потенциала в этом случае линейно убывает с расстоянием от центра, т. е.

t/=-,f (1.9)

Всякое статическое электрическое поле может быть представлено в виде суммы радиальных полей. Поэтому всякое статическое электрическое поле представляет собой потенциальное поле, т. е. пространство, каждая точка которого обладает вполне определенным потенциалом.

В линейной среде этот потенциал является суммой всех потенциалов, которые порознь образуются отдельными элементарными зарядами.

Поэтому во всяком электрическом поле можно мысленно провести поверхности, соединяющие точки с равными потенциалами. Эти поверхности называются эквипотенциальными поверхностями*.

Каждому потенциалу соответствует своя эквипотенциальная поверхность.

Очевидно, что эти поверхности нигде не пересекаются и в любой точке пространства каждая из них нормальна к электрической силе.

Также очевидно, что чем больше электрическая сила, тем на меньшее расстояние надо передвинуть заряд вдоль линий поля, чтобы совершить ту же работу. Другими словами, эквипотенциальные поверхности, проведенные через то же число единиц потенциала, тем ближе одна к другой, чем сильнее поле.

Электрический потенциал можно отсчитывать от любого потенциала, условно принятого за начало отсчета, т. е. за нулевой потенциал. Это вполне аналогично тому, что высоту на земном шаре мы можем отсчитывать от любой точки, высота которой принята за начало отсчета.

Часто за начало отсчета принимается средний потенциал земного шара; в других случаях потенциал какой-нибудь точки схемы.

Таким образом следует определять потенциал данной точки поля как работу, совершенную при переносе одной положительной единицы электричества из точки, потенциал которой принят за нулевой, в данную точку.

Работа, необходимая для переноса единицы электричества из точки с потенциалом в точку с потенциалом U, очевидно, равна разности U2 - U]., которая носит название разность потенциалов . С этим понятием, как известно, часто приходится встречаться.

§ 3. Статическая емкость.

Положим, 4TjD между двумя одинаковыми параллельными площадками 5 (фиг. 1.6), расположенными на расстоянии d, существует электрическое

поле, одинаковое во всех точках и направленное перпендикулярно к площадкам.

Силовой поток в пределах контура S будет

Ф=8В, (1.10)

где D электрическая индукция (т. е. число линий на 1 см).

Заменим D на еЕ, тогда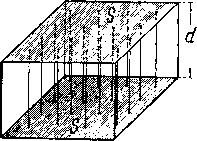

Фиг. 1.6.

щадками S обозначить через Я, то а следовательно.

Перепишем эту формулу так

Ф=5еЕ. (1.11)

Если разность потенциалов между пло-

ф = -

Величину

(1.12) (1.13)

(1.14)

мы будем называть диэлектрическим сопротивлением рассматриваемого участка пространства в направлении d, с боков ограниченного/ поверхностью, перпендикулярной S).

Для того чтобы заряды были расположены равномерно по поверхности s, надо, чтобы площадки S представляли собой часть очень больших взаимно параллельных металлических плоскостей, между которыми электрическое поле равномерно в области S.

Тогда можно определить также количество электричества Q, находящегося на площадках 5.

Каждая единица заряда испускает по принятому условию 4те линий.

Следовательно,

Величину называют емкостью.

В данном случае емкость, следовательно, равна

(1Л6)

Это-знакомое читателю выражение емкости плоского конденсатора. При выводе этого выражения мы подсчитывали, какое сопротивление оказывает среда силовым линиям потока.

1) По своему начертанию эта формула совершенно аналогична формуле для сопроти-

вления провода постоянному току

Различаются только коэфициенты е и f (диэлектрическая проницаемость и удельная проводимость).

Другими словами, мы подвергали исследованию не явления на обкладках конденсатора, а явления в среде, разделяЮJш;ей эти обкладки.

Это на первый взгляд мало заметное обстоятельство имеет огромное значение для правильного понимания природы явления, заключающегося в том, что емкость образуется н,е проводниками, служащими обкладками конденсатора, но тем пространством, в котором эти проводники находятся.

Из этого, в частности, следует, что, говоря о емкости каких-нибудь предметов (например, металлических шаров), можно применять это выражение только условно.

Не существует емкости предмета самого по себе, но всегда имеет место емкость между двумя предметами, или (говоря другими словами) емкость одного предмета относительно другого или многих других предметов.

Так например, говоря о собственной емкости уединенного металлического шара, надо подразумевать под ней емкость между этим шаром и всеми остальными близкими и далекими проводниками, на которых заканчиваются силовые линии, исходящие с поверхности шара.

§ 4. Вычисление статической емкости в простейших случаях.

Емкость, о которой мы говорили в предыдущем параграфе, называется статической емкостью, так как она относится к статическому электрическому > полю.

Вычисление статической емкости возможно только для относительно простых геометрических форм. В более сложных случаях получаются большие математические затруднения, и проще прибегнуть к прямому измерению или измерению на модели.

Укажем здесь два основных метода вычисления емкости.

Первый метод аналогичен тому, которым мы только что пользовались, и мы его применим для вычисления емкости шара.

Возьмем металлический шар радиусом Гу, показанный на фиг. 1.7 в разрезе, и окружим его другим концентрическим шаром с радиусом г. Тогда г - Гх будет измерять зазор между двумя шарами.

Вычислим диэлектрическое сопротивление между шарами. Для этого проведем внутри зазора между ними две концентрические сферы радиусами г и r-\-dr.

Так как промежуток dr бесконечно мал, то поле в нем можно считать равномерным и приложить к нему выражение для диэлектрического сопротивления, которое в § 3 было написано так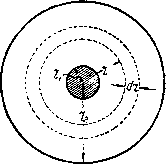

Фиг. 1.7.

(1.17)

Имея в виду, что S в данном случае есть поверхность сферы с радиусом г, напишем

откуда

(1.19) 35