i = f(a)

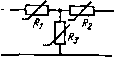= /(0

-1 W

Окончание табл. 2.5

G<2)

1 -2

2 -1

G<3>

-3 3 -1

-1 3-3 1

;(2)

2-1 +

G<2)

G<3)

G(3) .

3 -1

G</

-1 3-31+-

Аналогично поз. 1

1+3 3

1 3 3 1-

Аналогично поз. 1

Аналогично поз. 2

G(3) = -i- f (u) = Y/oe =

(2.24)

G(2)

0(1)

(2.25)

Таким образом, обобщенные параметры диода в рабочей области не зависят от величины управляющего тока.

Условимся характеризовать нелинейные свойства диода при заданном значении управляющего тока io с помощью обобщенных параметров GV и G()/G(). Из соотношений (2.24) следует:

2. Соединения диодов

На рис. 2.13 приведены возможные последовательное (а) и параллельное (б) соединения диодов.

Для последовательного соединения одинаковых дио-

где Ы 1 - напряжение, приложенное к одному диоду, откуда

=-fo-. G< = 4--o; G<> = 4--o. (2.26)

Рис. 2.13.

Т>Ш-----С>К>Ьт -

Из формулы (2.26) получим:

G Y . 0(3) .у, qC) 2га 0(1) ~ 6rt2

(2.27)

Сравним одиночный диод и соединения п диодов по обобщенным параметрам при удовлетворении одной и той же проводимости GO нелинейной цепи. Тогда

т. е.

12й = П1\о.

(2.28)

Таким образом, удовлетворение заданной проводимости G(>) требует однозначного подбора токов одиночного дио-

да iio и последовательного соединения ijo в соответствии с выражением (2.28).

Рещив соотношения (2.25), (2.27), получим, что переход к последовательному соединению уменьшает обобщенный параметр по второму порядку в п раз, а по третьему в раз. Таким образом, выигрыш от последовательного включения диодов равен соответственно В2=п и

Для параллельного соединения одинаковых диодов i=n/oeV ,

откуда

т. е.

GO) = nyio, G(2) = G(3) = (2.29)

g v . g3) f ~ 2 g(I) ~ 6

Хотя переход к параллельному соединению при заданной величине GO требует подбора тока io=G(VrtY> однако это не влияет на обобщенные параметры [см. формулы (2.29) и (2.25)].

3. Комбинации диодов и линейных резисторов

На рис. 2.14 приведены простейшие схемы подобных комбинаций: последовательной и параллельной.

Рис. 2.14.

Для схемы рис. 2.14, а в рабочей области i = /oev( -ifi),

откуда можно получить:

G<4 =

(l + Y o/?)=

G(3) =

(1 + yW

Из соотношений (2.30) следует;

G = L y g> J yl-2yitR)

gO 2 (1 + yioR) g<> 6 (l+yioR)*

(2.30)

(2.31)

Таким образом, в соответствии с выражениями (2.31) увеличение линейного резистора R приводит к уменьшению обобщенных параметров нелинейности, при этом параметр третьего порядка имеет нулевое значение при некотором токе i*=\/2yR. Физическая сущность последнего явления заключается в том, что на элементе схемы, показанной на рис. 2.14, а, возникает взаимодействие нелинейных продуктов, обусловленных параметрами как второго, так и третьего порядков, причем при токе i* это

взаимодействие сопровождается их взаимной компенсацией.

Аналогично п. 2 оценим выигрыши Вг и Вз при одной и той же проводимости цепи GC). Приравняв GO одиночного диода из соотношений (2.24) и GO из (2.30), получим

Используя формулы (2.29) и (2.31), найдем: 1 1

(1-Gi?)

Вя =

(\-GRf {1-3GR)

Характер зависимостей Вг и Бз в области малых G, т. е. в рабочей области, для последовательной схемы приведен на рис. 2.15, где для Bj G*=l/R, для Вз G0)* = = 1/37?. Из последних зависимостей следует, что Вг и Вз значительно возрастают вблизи G<)*. Таким образом, схему рис. 2.14, а следует использовать в тех случаях, когда необходимо уменьшить НИ при относительно больших величинах GO. Так, например, в схеме Г-образного УЭА (см. рис. 1.6, б) в режиме АРУ при малых передачах тракта практически все входное напряжение оказывается приложенным к резистору Ri. В качестве этого элемента

целесообразно использовать схему рис. 2.14, а, где

R~l min = R-

Для схемы с параллельным включением (см. рис. 2.14, б) GO) = Y<o + -, в то время как G<2> и G*) оказываются равными тем же параметрам для одиночного диода. До-

пуская, что проводимость G<> при включении R не изменяется, что требует подбора тока Io = . находим выигрыши

Зависимость Вг и Вз приведена на рис. 2.16, где G()**=l/7?. Таким образом, последняя схема дает наибольший эффект при относительно малых величинах GO. Включение дополнительных резисторов, а также нескольких диодов влияет также на диапазон изменения проводимости эквивалентного управляемого элемента и, следовательно, на величину D УЭА, мощность, потребляемую от источника управления, шумовые свойства УЭА и т. д. Поэтому окончательное суждение о целесообразности схем, представленных на рис. 2.13, 2.14, можно сделать лишь с учетом этих факторов.

4. Нелинейные емкости

Обычно в УЭА используют в качестве нелинейных емкостей варикапы, у которых барьерная емкость р-п перехода Cj аппроксимируется выражением (1-7):