Агатах =

J. !+2e (l-max)

4(/

(1+6)2

П\ (2.50)

ЛгЗтах -

(1 + 6)

,max)P£)4 (2.51)

г2тах -

D\ (2.52)

Аналогично для случая АРУ можно получить, что максимум искажений происходит при = ща:

Vml e[l-f 29и(1-Щ

. tvQ ел 14-е (1 -щ-е П+2еи(1-иахЖ п2 /о i;c,4

ЙгЗтах - (Г+ёР-

Из анализа соотношений (2.50) и (2.53) следует:

1) сопротивление истока увеличивает нелинейные искажения и сокращает величину динамического диапазона D при заданных максимальных искажениях;

2) максимальные искажения при РРУ меньше искажений при АРУ приблизительно в * раз;

3) для уменьшения искажений и расширения динамического диапазона следует выбирать транзисторы с большей величиной напряжения отсечки f/o;

4) расширение динамического диапазона регулятора приводит к увеличению нелинейных искажений.

Для схемы рис. 2.21, г уравнения имеют вид:

1 = U2 + U2; icl=c2 = ; cl = fl( 2); ic2 = /2( 2),

откуда в режиме РРУ

Йг2 =

2e (i-y-2[i+2e (i-y]+i±s4

1 - Sa

*гз = --г {(1 - 21,) [40 (1 -1,) (2 - i,) I, +

+ 4в (1-у+ 1]+0 [(1 уз + + 3(l-y-3(l-y-Il}.

где а =

1 + 2=1; с;

t/yg - вели-

чины, относящиеся к соответствующим транзисторам; в ре ЖИМ6 АРУ

4{/о

1+29(1-у

(1-аР

- 2П+И1-У1 +29 (1-2у};

.{(1-2 [4е (i-Sa)M2-y I2+

(2.54)

+ 40Л1 - У + 1] + в [(1 - 3 (1 - У-

-3(1-У-1]}.

Введя динамический диапазон аттенюатора Д из выражений (2.54) получим: для РРУ

Йг2тах -

ЙгЗтах -

i + J + 4e-

(2.55)

для АРУ

A;2max = (1 -f 2 1+5 + 28

КгЗтах = -- L>

0-2 + i+49S=->

+ e 1 +

(2.56)

Сравнение соотношений (2.47) и (2.48) с (2.54) - (2.56) показывает, что схема с двумя транзисторами при одном и том же динамическом диапазоне дает большие нелинейные искажения.

Характеристика нелинейных искажений регулятора на ПТ по схеме рис. 2.21 приведена на рис. 2.23. Здесь используется полевой транзистор типа К.П103И с 1 = = 100 мВ, ., = 22 кОм, {/о = 2В, /со=1,6 мА.

Аппроксимация вида (2.32) удовлетворительно отражает поведение ПТ в ненасыщенной области и дает хорошее совпадение расчета и эксперимента УЭА, в том чис-

ле по критериям нелинейности для 0,7-0,8. ние аппроксимации для больших значений <1 жено Р. М. Коробовым и Л. Н. Крымером [23].

Уточне-предло-

W 0.6 0,4

0.2 0.1

0Р2 0.01

Рис. 2.23.

0,2 , O.f

0,8

2.3. ЧАСТОТНЫЕ СВОЙСТВА УЭА

Частотные зависимости коэффициента передачи УЭА, включенного в заданное сечение тракта, определяются следующими факторами:

1) реактивными параметрами управляемых компонентов (для емкостных УЭА - нелинейными емкостями, для резистивных - паразитными емкостями и индуктив-ностями, см. § 1.5);

2) другими паразитными элементами схемы и конструкции УЭА (емкостями и индуктивностями соединительных цепей, паразитными элементами цепей связи - трансформаторов, автотрансформаторов и т. д.);

3) разделительными конденсаторами;

4) комплексным характером импедансов источника сигнала и нагрузки.

Достаточно полная схема замещения УЭА, в особенности для высоких частот, сложна и обычно затрудняет ручной анализ ее частотных свойств. Трудности анализа усугубляются двумя причинами: во-первых, изменением активных и реактивных элементов в УЭА в процессе его работы; во-вторых, зависимостью частотных свойств от уровня сигнала, который в частных случаях может вывести нелинейные элементы УЭА из области, где справедливы малосигнальные трактовки процессов. Последний режим мы, однако, рассматривать не будем, считая его нехарактерным для многих применений УЭА в прием-

но-усилительных трактах. Некоторые вопросы режима большого сигнала изложены в работе [33].

Окончательные результаты анализа частотных свойств УЭА могут быть представлены в двух вариантах: в виде семейств АЧХ (ФЧХ), построенных в двумерном пространстве, с параметром в виде коэффициента передачи /Со на заданной частоте или диапазона его изменения D = KomuJKo (рис. 2.24, а); в виде того же семейства,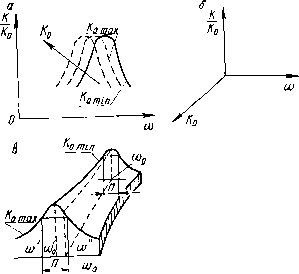

Рис. 2.24.

но в трехмерном пространстве с координатами К/Ко (ф), (О, К (D) (рис. 2.24,6, в).

В общем случае, как следует из рис. 2.24, в процессе регулирования изменяются такие параметры частотной характеристики тракта, как резонансная частота или частота квазирезонанса ио, полоса пропускания П, граничные частоты 0) и ш , крутизна склонов АЧХ (ФЧХ), а также форма частотных характеристик. Анализируя Деформации конкретных АЧХ и ФЧХ, следует сделать вывод об их допустимости в заданном диапазоне D, а в случае невыполнимости технических условий на УЭА определить пути стабилизации частотных свойств тракта. Хотя подробный анализ частотных свойств всегда может быть осуществлен с использованием ЭЦВМ, однако для

простейших случаев можно применять ручной расчет и сделать выводы о возможностях улучшения частотных свойств УЭА. В основе этого анализа лежит использование универсальных выражений для коэффициентов передачи (см. п. 2.1.1 и табл. 2.5), но вместо GO и /?.) следует подставить комплексные величины УО и 20 соответ-

ственно.

Рис. 2.25.

Рассмотрим, например, простейшие структуры УЭА с одним управляемым резистором: параллельным (рис. 2.25, а) или последовательным (рис. 2.25, б). Условимся учитывать на соответствующей схеме замещения паразитные емкости управляемых резисторов, в общем случае переменные (С~), и элементы входного иммитанса нагрузки G и С ,.

Нетрудно показать [24], что для цепи с параллельным включением управляемого резистора (см. рис. 2.25, а)

= = [1 + 1 (G~ + GJ (1 + /(от )]-\

т =(С~ + Сз,) (G~ + G )-4

Отметим, что емкость открытых диодов изменяется в первом приближении прямо пропорционально току i, т. е. примерно так же, как и их проводимость (2.29). Если при этом обеспечивается равенство

(2.57)

то форма частотной характеристики УЭА в процессе регулирования током i изменяется незначительно. Для малых коэффициентов передачи

HL = (1/1 + (сотз,))-!.

Для схемы с последовательным включением диода (см. рис. 2.25,6)

\К\ л/ l + (u)C~/G~P

Если условие (2.57) выполняется, то в цепи по схеме рис. 2.25, б автоматически обеспечивается коррекция частотной характеристики УЭА аналогично известному случаю компенсированных делителей напряжения. Разумеется, это происходит в той области частот, где справедлива схема замещения рис. 2.25, б и выполняется равенство (2.57).

В работе [9] выполнен анализ частотных свойств Г-образного УЭА с двумя нелинейными резисторами, имеющими паразитные емкости (см. рис. 2.25, в).

Ниже приведены окончательные формулы для расчета наибольших допустимых емкостей С\ и Са + Со, обеспечивающих допустимую степень изменения АЧХ, ФЧХ и отклонения входного сопротивления УЭА от заданного значения /?bi=/?o:

max

<йтах о (А(р)доп

\ Увх /доп

тахО

где (flmai - максимальная рабочая частота; Ув1= 1/о.

В заключение следует отметить, что рассмотрения простейших приведенных выше случаев, однако, недостаточно для суждения о частотных свойствах современных приемно-усилительных трактов с УЭА, к которым предъ-