тельной ветви, что способствует уменьшению НИ в тракте УЭА.

Из соотношения (2.41) получаем также, что ka максимален при малых Ki2 и при /Ci2< 1 от его величины практически не зависит, при этом

ЛгЗтах - J2 yUmaux-

В режиме РРУ

откуда для диода

Характер зависимости \к т21 от приведен на рис. 2.19,

I Аг2тах - jg

(2.43)

Из сравнения выражений (2.40) и (2.43) следует, что ггшах в параллельном регуляторе, работаюш,ем в режиме РРУ, оказывается в 4 раза меньше, чем в последовательном, причем вид зависимости Аа от /Си (D) для этих вариантов схем существенно отличается.

Связь к гз с величиной Кп оказывается сложной:

/ггз = (1 - Ки) (2 - гКп) Khul и имеет максимум при/Ci2 = 5/6.

3. НИ в УЭА с несколькими управляемыми резистивнми нелинейными элементами

Расчет НИ в схемах сложных УЭА следует осуществлять с использованием методов, изложенных выше в пп. 2.2.1, 2.2.2. Хотя эти расчеты не вызывают принципиальных трудностей, однако они носят частный характер, т. е. относятся к конкретной структуре УЭА и характеристикам используемых нелинейных компонентов. В некоторых случаях расчеты можно упростить, получив предварительно ряд универсальных характеристик, пригодных для расчетов устройств определенного класса. Покажем

это на примере класса УЭА с неизменным входным сопротивлением в диапазоне регулирования /?вх=/?о (см. п. 2.1.2). Допустим, что в рабочем диапазоне частот инерцией элементов УЭА можно пренебречь. Например, как показано в работе [И], коэффициент второго порядка ряда (2.13) можно представить в виде

(2.44)

где gP -нелинейный параметр второго порядка i-ro нелинейного элемента (см. табл. 2.6); л: ер, - линейный коэф-Гциент передачи от места включения i-vo нелинейного элемента УЭА до его выходных зажимов.

Таблица 2.7

Схема

Нормированная функция Кр Рг> нелинейности УЭА

Рис. 1,6, в Рис. 1.6, г Рис. 1.6, а

Рис. 1.6, е Рис. 1.6, и Рис. 1.6. к

- = 4-(1-К)3(2-К); = --8

(1-К)М1 + ЗК) . 4 (1 + КГ

(1 К)М1-) 16(2 -К)

-gv-64

Используя предложенный в работе [Щ способ опре-. Г можно получить универсальные выражения Г2?)ТсГветств7ющие им нормированные харак Йристики коэффициентов (рис. 2.20) для различных эле-

ментов ряда типовых структур УЭА (а-для схемы рис. 1.6, в; б - для схемы рис. 1.6, е; в ~ для схемы рис 1 6 г-г -для схемы рис. 1.6,к; d - для схемы рис 16 д-е - для схемы рис. 1.6, и). .

\ Ra ° 15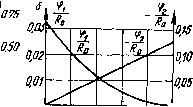

016 0.12 О.Од

о 0,2 0.6 О.в 10 К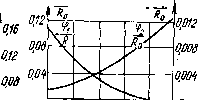

о 0Z Q.t 0,6 0,8 W К е Ъ

0,006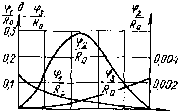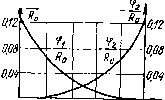

о 0,2 0.f 0.6 0,в 1,0 К

О 0,2 0,4 0,6 0,д 1,0 К

Рис. 2.20.

Анализируя табл. 2.7 или рис. 2.20 с учетом выражения (2.44), можно оперативно оценить поведение коэффициентов нелинейной передаточной характеристики УЭА во всем диапазоне регулирования, определить неблагоприятные с точки зрения НИ области его изменения и требования к нелинейным элементам.

Проиллюстрируем вышеупомянутый метод расчета МИ второго порядка на примере Г-образного УЭА с двумя нелинейными элементами в виде диодов (см. рис. 1.6, в), удовлетворяющего условию /?вх = /?о- Параметры G2:

В соответствии с функциональной связью F{Vi, V2) =0 табл. 2.1 находим требуемый закон изменения:

где i=Ioe .

Из соотношения (2.45) можно получить

fii 1

(2.45)

М2) dh dui

Опуская дальнейшие расчеты, приведем окончательное выражение для а):

, (2.46)

где знаки ± относятся к различным способам включения диодов друг относительно друга, что, естественно, влияет на взаимодействие НИ, обусловленное Gi и Ga, и, следовательно, на выходной эффект.

Используя формулы (2.48) и (2.18), можно получить

где А - коэффициент, практически близкий к единице (0,5-1). Из последнего выражения следует, что при малых Ki2 ггатах ~ AU gay и не зависит от D. Из сравнения kj. одноэлементных и двухэлементных УЭА следует, что искажения в последних оказываются одного порядка с искажениями в одноэлементных УЭА с параллельным нелинейным резистором (см. рис. 2.17,6).

4. НИ в УЭА на основе полевых транзисторов (ПТ)

Рассмотрим НИ в наиболее употребляемых схемах УЭА, использующих регулируемую выходную проводимость ПТ: с одним (рис. 2.21, а) и двумя (рис. 2.21, s) ПТ. Эквивалентные схемы для обоих случаев приведены соответственно на рис. 2.21, б и 2.21, г.

Используя метод, изложенный в п. 2.2.1 [11], составим систему уравнений для схемы рис. 2.21,6, введя на ней соответствующие обозначения и выделив из ПТ внутренний транзистор ВТ и сопротивление истока (рис. 2.22):

2+ия = 1; UR=icR;

ic = f ( си, з.и),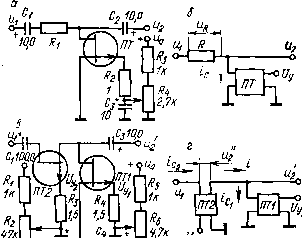

г гТ 0,0-Г

Рис. 2.21.

откуда подсистема первого порядка: Ки2 + K\cR = 1;

Aic - 2il\u2 I

подсисте1*{ы высших порядков:

KiV + K\R = 0;

где Y (P) - CM. в табл. 2.3 (первичные нелинейные параметры берутся из поз. 7 табл. 2.6). Опуская промежуточные расчеты, приведем окончательные выражения ча-

стных коэффициентов гармоник для режимов АРУ и РРУ: для РРУ

Umi e[i-f2еи(1-)] . AUo [1 + е(1-?)р

е [1 + е (1-)]-е[1 + 2ел1-1)?

k,2 =

Рис. 2.22.

(2.47)

для АРУ

fer2 =

4£/о

е[1 + 29и(1-)] [1+6(1-1)1

tLe e [i + 9(i-g)]-e[i + 29 (i-i)p

11+в(1-Е)р

(2.48)

Величина коэффициента передачи схемы и

v тг

-пл.

1+6(1-1)

Оценим динамический диапазон регулирования:

(2.49)

и свяжем его с максимальным коэффициентом нелинейных искажений (2.47).

Из соотношений (2.47) следует, что максимум искажений при РРУ соответствует = 1п,ах. откуда, используя формулу (2.49), нетрудно получить: