и \

где Со - начальная емкость перехода (приотсутствии приложенного внешнего напряжения).

Представив полное напряжение и в виде постоянного смещения L/= и малого переменного напряжения и, приходим к выражению

(2.32)

Разложив соотношение (2.32) в ряд для х<1, получим

1 , П(П-\- I) 9

1 - [А + - 2! 1 -

ИНОЙ емкое

где параметры нелинейной емкости

nioo .

или для п = 0,5 (диоды с резким переходом)

л( +1)С

для rt = 0,33 (диоды с линейным переходом)

9 ({/ + f/=)

G<2 = Gaa = -(f/y-i/o);

G<2> = 0,

где f/y = U3.h.

В табл. 2.6 для удобства использования приведены выражения для нелинейных параметров различных нелинейных элементов, применяемых в УЭА.

2.2.4. Нелинейные искажения в некоторых схемах УЭА

/. НИ в УЭА с последовательным управляемым нелинейным, резистивным элементом (рис. 2.17, а)

Используя формулы (2.22), (2.23) и поз. 3 табл. 2.5, получим:

Г2Л19 а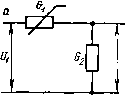

и, и,

5. Полевые транзисторы

В УЭА широко используют выходные проводимости полевых транзисторов (ПТ), управляемые напряжением затвор - исток из. (см. § 1.5).

Зависимость тока стока Ic внутреннего транзистора ВТ в рабочей для УЭА области обычно аппроксимируется выражением (1.8).

Используя его, легко найти первичные параметры ВТ вблизи начала системы координат, когда с.и-О:

Рис. 2.17.

где Ки = -[ = Gi + Gi ~ коэффициент передачи УЭА на рис. 2.17, а.

В режиме АРУ в соответствии с выражениями (2.33) и (2.18):

(2.34)

2G2/(?2

№ поз.

Характер нелинейности

Резистивный

РезистивныЯ

Резистивный

rt>h

Характер нелинейной зависимости

в; С

Примечания: 1. Для 1 = /(м) параметры - коэффициенты ряда фициенты ряда С = Со + Ci +г *-

12 L

твых*

(2.35)

Как следует из соотношений (2.34) и (2.35), йг2 и *гз увеличиваются с уменьшением коэффициента передачи УЭА Ki2- Это связано с тем, что в схеме рис. 2.17, а с падением К\2 увеличивается падение напряжения на нели-

Таблица 2.6

Резистивный

Резистивный

Емкостный

Резистивный

гЙ-1

Для ВТ полевого транзистора

= /( )

C = f{u)

1 + yioR

Yo +

2(1+Ye f

яС ,

Y%(l-2v J?) 6(1+yW

n (n + 1) Coo

21 (9K + t/=)=

I = G<>u + Gm* + G< *. 2. Для C = f{u) параметры - коэф-

нейной проводимости Gi, что приводит к возрастанию НИ. Поэтому предельная величина диапазона регулирования Z)max= l/%2min Определяется максимальной величиной допустимых НИ. Для D> 1:

*г2тах

*гЗтах

2G, G<3>D,

/ПВЫХ1

и твых-

(2.36)

При регулировании в УЭА величины G<2) и С(3) изменяются, следуя за изменением управляющего воздействия. В соответствии с табл. 2.6 для одного диода:

(2) уч уа

(3) уч

Но величина G*i связана с 0 = l/ZC =откуда

i = -D%l- (2.37)

Из соотношений (2.36) и (2.37) следует:

и уРщахтвых .

г2тах---,

гЗтах -

f max тъых 24

(2.38)

(2.39)

В режиме РРУ в соответствии с формулами (2.25), (2.19)

Г2 -

2Gj/Cis

откуда получаем, что fersmai соответствует минимуму и для Z) l:

*г2шах

или для диода

Хг2тах--1-

(2.40)

Можно показать, что полное выражение для kJ имеет

,- Yd-а: ) г,

Кг2--4 и ,

т. е. при уменьшении Кц г2 монотонно возрастает, однако для малых Кц (т. е. больших D) его величина практически не зависит от абсолютной величины D.

2. НИ в УЭА с параллельным управляемым нелинейным резистивным элементом (рис. 2.17. б)

Используя выражения (2.22), (2.23) и поз. 3 табл. 2.6, получим:

Выполнив расчеты, аналогичные расчетам для случая последовательного нелинейного элемента, находим для АРУ и диода:

I Лг2 1 = 4(1 - )

kr3=il-K ) (2-3/Cia)f/L.x.

(2.41)

Характер зависимости кт2 от К]2 показан на рис. 2.18. Из рисунка находим, что при малых К12 величина йгг стремится к

(2.42)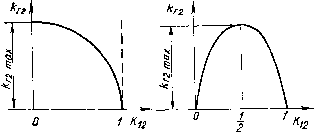

Рис. 2.18.

Рис. 2.19.

Из сравнения выражений (2.42) и (2.38) следует, что максимум НИ в схеме с параллельным регулятором оказывается в Dniax раз меньше, чем в схеме с последовательным регулятором. Это объясняется тем, что в случае параллельного включения нелинейного элемента практически все выходное напряжение оказывается при малых Ki2 приложенным к линейному резистору в последова-