Здесь i-я скобка представляет собой вклад метрики Фано на 1-м кадре

Для каждого рассматриваемого пути в i-м кадре требуется вычислять только этот член. Метрика р, (с ) получается прибавлением нового приращення к метрике Фано пути, который записан на предыдущей итерации в вершине стека.

12.4. Алгоритм Фано

В алгоритме Фано требуется знать среднюю расходимость на кадр правильной последовательности d или хотя бы верхнюю границу для d. Это предполагает наличие некоторой меры статистической регулярности расходимости, так что средняя расходимость может быть использована как типичная. Пока алгоритм Фано следует по правильному пути, можно ожидать, что в пределах первых / кадров расходимость равна примерно dL Алгоритм допускает несколько ббльшую величину расходимости, но если она намного больше, то алгоритм сделает вывод, что он на неправильном пути. Выберем (быть может, моделированием) некоторый параметр d , больший, чем tf, и определим перекошенное расстояние формулой )

t (/) =dl-d (О,

где d (/) равно расходимости текущего пути-претеидента на дереве. Для правильного пути d (/) приблизительно равно dl, а t (1) положительно и возрастает. Алгоритм следует по пути на дереве до тех пор, пока t (1) возрастает. Если вдруг t (/) станет уменьшаться, алгоритм заключает, что в некоторой вершине он выбрал ошибочное ребро и возвращается по дереву обратно, проверяя другие пути. Он может найти лучший путь и следовать по нему или может возвратиться к той же самой вершине, но уже более уверенно продолжать путь через нее. Для того чтобы решить, когда t (/) начинает уменьшаться, в алгоритме Фано используется переменный порог Т, который всегда кратен приращению А порога. Пока алгоритм движется вперед, порог, оставаясь не больши.м t (1) и кратным приращению Д, принимает максимально возможное при этих ограничениях значение. Благодаря тому, что Т квантуется с шагом А, допускается небольшое убывание t (/) без пересечения порога.

) в этом выражении знак выбран так, чтобы правильной работе алгоритма соответствовало положительное значение расстоиния.

В алгоритме Фано требуется, чтобы q ребер, выходящих из каждой вершины, были перенумерованы согласно некоторому правилу упорядочивания. Это правило ставит в соответствие

каждому ребру индекс /, / = О..... ? - 1- Нет необходимости

запоминать эти индексы в каждом ребре; достаточно знать правило, по которому при возвращении алгоритма в вершину по ребру с известным индексом ; он может переупорядочить ребра, найти ребро / и затем найти ребро с индексом j + \. Наиболее общим правилом является правило минимального расстояния. Ребра упорядочиваются в соответствии с их расстояниями до соответствующего кадра заданного слова, а неопределенность разрешается по любому удобному подправилу. Однако алгоритм будет правильно работать при любом фиксированном порядке ребер.

Фиксированное правило упорядочивания может привести к более длительному поиску назад-вперед, но освобождает от необходимости вычисления и перевычисления при достижении каждой вершины. Какое правило упорядочивания более просто в реализации, зависит от деталей конструкции. Для простоты понимания структуры алгоритма правило упорядочивания лучше оставить несколько неопределенным; предположим только, что в каждой вершине ребро, ближайшее к ребру данных, занумеровано первым. Алгоритм будет отыскивать ребра из каждой вершины в соответствии с этим правилом.

Основанная на регистрах сдвига реализация алгоритма Фано показана на рис. 12.10. Основой реализации является копия машины с конечным числом состояний, которая на рисунке представлена регистрами сдвига; к ним добавлено несколько вспомогательных запоминающих регистров. Алгоритм пытается подать символы в копию машины с конечным числом состояний таким образом, чтобы на ее выходе сформировалась последовательность, достаточно близкая к заданной последовательности. На каждой итерации алгоритм имеет доступ к самому последнему кадру, введенному в копию машины с конечным числом состояний. Он может изменить символ в этом кадре, вернуться к более раннему кадру или ввести новый кадр. Что именно делать, алгоритм решает на основе сравнения величины перекошенного расстояния I (1) и текущего значения порога Т.

В упрощенной форме алгоритм Фано показан на рис. 12.11, Практические детали, связанные с конечностью размеров буфера, временно игнорируются.

Если последовательность данных близка к генерируемой последовательности, то алгоритм будет циркулировать по правой петле на рис. 12.11, и при каждом цикле все регистры на рис. 12.10 сдвигаются на один кадр вправо. До тех пор пока / (/) остается выше порога, алгоритм продолжает сдвигаться вправо и повышать

(опия источник

f-ичный регистр сдвига \

вы од -С ноль

♦ i i

Логина источника

ДооавлеиныО 6yipep

расстояния

Влая

. Команды на сдвиг .!/ возрастание

Добавленный буфер

б кадров

Рис. 12.10. Реализация алгоритма Фано на регистрах сдвига.

порог так, чтобы тот оставался близким Kt (I). Если t (I) спзскается ниже порога, то алгоритм Фано проверяет альтернативные ребра этого кадра, пытаясь найти то ребро, которое делает t (/) выше порога. Если ему не удается сделать этого, то он возвращеется назад. Как мы увидим в дальнейшем, если алгоритм начал возвращаться обратно, то логика заставит двигаться его назад до тех пор, пока не будет найден альтернативный путь, который находится над текущим значением порога, или вершина, в которой был установлен текущийпорог. Затем алгоритм снова движется вперед с уже пониженным значением порога; но теперь, как мы убедимся позднее, порог не повышается до тех пор, пока алгоритм не придет в новую, ранее не рассматривавшуюся вершину. Каждый раз, когда алгоритм, двигаясь вперед, посещает ранее исследовавшуюся вершину, он имеет меньший порог. Алгоритм никогда не посетит одну и ту же вершину дважды с одинаковым значением порога. Следовательно, он может посещать любую вершину только конечное число раз. Это поведение гарантирует нас от зацикливания алгоритма; он должен продолжать движение вперед по последовательности данных.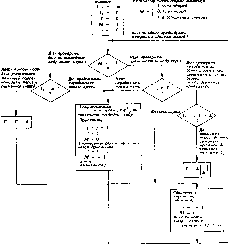

Рис, 12.11. Аннотированная блок-схема алгоритма Фано.

Замечания: Кадры индексированы указателем кадров /. Итерации не нндекснрованы. Ответвлевня от текущего узла индексированы с помощью /

Теперь необходимо доказать два сделанных ранее утверждения: 1) если алгоритм Фано не может найти альтернативный путь, то он движется назад к вершине, в которой было установлено текущее значение порога, и понижает его; 2) алгоритм не будет повышать порог до тех пор, пока не достигнет ранее не исследовавшегося узла. Что касается первого утверждения, очевидно, что если алгоритм Фано не может найти ребро, от которого он должен двигаться вперед, то он в конце концов должен вернуться в указанную вершину. Но если в предшествующем некоторой вершине кадре перекошенное расстояние / (г - 1) меньше текущего значения порога Г, то порог был увеличен в 1-ш кадре. В блок-схему на рис. 12.11 включен этот тест для нахождения вершины, в которой был установлен текущий порог; теперь в этой вершине порог уменьшается.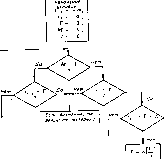

М - О-в протибие М- - 1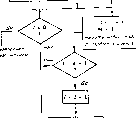

Если возможно, уменьшить и Тat

Рис. 12.12. Алгоритм Фано.

ров вперед. Если алгоритму удастся найти правильную вершину, то он сможет перенасгроиться. Это возможно, если заданная последовательность содержит достаточно длинный сегмент, в котором генерируемая последовательность с ней в точности совпадает.

Задачи

12 1 Пать поостую формулу метрики Фано для случая, когда разность между ГноГГполуПной последовательностями задается гауссовским шумом с независимыми и одинаково распределенными отсчетами.

Для доказательства второго утверждения заметим, что по того, как порог понижен на Д, алгоритм Фано ищет ребра в том же порядке, что и до .этого, до тех пор, пока не найдет MecToJ в котором перекошенное расстояние, ранее бывшее меньше п№ рога, становится больше него. До этого места порог Г изменитьс1( не может. Это происходит из-за того, что после понижения по рога на Д перекошенное расстояние в тех вершинах, где оно превышало первоначальный порог, никогда не будет меньше Т -t- Д. Когда алгоритм продвигается в новую часть дерева, он в конце концов достигает состояния, в котором i (1 - 1) < < Г -f Д и i (1) Т. В этой точке порог повышается. Это является тестом для определения того, что алгоритм посетил новую вершину и нет необходимости помнить точно все посещен-! ные ранее вершины. Этот тест включен в схему на рис. 12.11.

Алгоритм Фано зависит от двух параметров р и Д, которые) можно выбрать моделированием на ЭВМ. Практически необхо*! димо время от времени уменьшать t (1) к Т так, чтобы эти числа! не становились слишком большими. Вычитание из обеих величие некоторого числа, кратного Д, не влияет на последующие вы.: числения. . .

В практической реализации существенен также выбор ши4 рины окна Ь. На рис. 12.12 приведена более полная блок-схем* алгоритма Фано, от-ображающая важную роль параметра ЬЛ Каждый раз, когда самый старый кадр достигает конца буфера, что отмечается указателем кадра, он выходит из окна, а указа-! тель кадра изменяется так, чтобы всегда указывать на самый! старый имеющийся кадр. Иногда алгоритм может попытаться! вернуться назад так далеко, что отыскиваемый им кадр оказы- вается уже выведенным. Такое явление называется переполне нием буфера и случается, когда указатель кадров принимав отрицательные значения. Переполнение буфера является су- щественным ограничением алгоритма Фано. Во многих приложе ниях вероятность переполнения буфера так медленно убывае с ростом размера буфера, что вне зависимости от того, насколькй! большим выбран буфер, эта проблема полностью не снимаетсяЖ

Существует два способа управления переполнением буфера Наиболее надежным является периодическая Подача на вход машины с конечным числом состояний известной последователь*! ности переходов, длина которой равна длине кодового огран1Г чения. Если буфер переполнится, то алгоритм декларирует отка и ждет начала следующей известной ему последовательности при котором он снова начинает работу. Все данные, поступивши между моментом переполнения буфера и следующим включением,! теряются.

В случае, когда длина кодового ограничения не слишком ве лика, альтернативный путь состоит в движении указателя ка