V-V ь

Рис. 12.7. Принципна.1ьный вид алгоритма Витерби,

чаются ситуации, когда принять однозначное решение и отбросить кадр ie удается либо потому, что имеется несколько ближайших путей, либо потому, что ширина окна Ь слишком мала для принятия решения. Тогда используется некоторое правило разрешения этой неопределенности. Такое событие случается пренебрежимо редко. Вместе с ростом числа кадров растет расходимость каждого пути. Чтобы избежать переполнения памяти, приходится время от времени редуцировать расходимость. Простое правило такой редукции дается вычитанием наименьшей расходимости из всех расходимостей. Это не влияет ва выбор минимальной расходимости.

Полезно представлять себе декодер Витерби как окно, через которое можио наблюдать часть решетки. Это иллюстрируется рис. 12.7. На рисунке можно видеть только часть решетки конечной длины, на которой отмечены выжившие пути и их расходимости. С течением времени решетка скользит влево. При появлении справа новых вершин некоторые пути продолжаются в них, а другие исчезают; самый старый столбец выходит из-под наблюдения налево. Со временем левый столбец вершин исчезает, и лишь для одной из его вершин будет существовать проходящий через нее путь.

На рис. 12.8 приведен пример. Для простоты и метки на решетке, и последовательность данных в примере выбраны двоичными. Евклидово расстояние заменяется просто числом позиций, в котором различаются две посчедовательности. Выберем ширину окна b равной 15. Предположим, что заданная последовательность равна

V = 101000001000000000000000

и требуется найти путь на решетке, ближайший к заданной последовательности.

Диаграмма состояний декодера показана на рис. 12.8. На третьей итерации алгоритм находит ближайший путь к каждой вершине третьего кадра. Затем, продолжая пути, ведущие к вершинам (г ~ 1)-го кадра, и сохраняя ближайший путь к каждой вершине г-го кадра, а.чгоритм на л-й итерации находит ближайшие пути в вершины г-го кадра. Иногда может возникнуть неопре-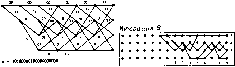

Шерация

Итерация 4

Итерация 5

Чтерация 6

Итшаиия 7

Итемшя 8

Итерация Ю

Итерация и

Итерация >2

о 2 } i Ь 1 й

{терация /3

1терация t4

4 s * j 8 <! № il и 13 *

Итерация IS

5 6 7 8 9 10 ii 1г i

Рис. 12.8. Пример алгоритма Витерби.

деленность. В данном примере имеются две неопределенности в пятой итерации.

Алгоритм может разрешить неопределенность случайным образом или сохранить оба пути, относительно которых существует неопределенность, В данном примере неопределенность сохраняется до тех пор, пока не находится лучший путь или сомнительный участок не выводится за пределы буфера. Если имеется только один путь, проходящий через вершину наиболее старого кадра, то принимается однозначное решение.

В этом примере ближайшей к данной последовательности будет либо нулевая последовательность., либо последовательность с началом 1110001011000... . \

Истинная реализация рассматриваемого алгоритма может сильно отличаться от приведенного на рис. 12.8 символического описания. Например, выживающие пути на решетке можно задавать в виде таблицы 15-битовых чисел. При каждой итерации некоторые из этих 15-битовых чисел сдвигаются влево, выталкивая наиболее левый бит и добавляя справа новый бит. Другие из 15-битовых чисел этого списка не видоизменяются, а выбрасываются из списка.

12.3. Стек-алгоритм

Для больших решеток алгоритм Витерби быстро становится непрактичным; при длине кодового ограничения 10 алгоритм требует запоминания 1024 путей-претендентов. Для того чтобы ослабить влияние больших длин кодового ограничения, была разработана стратегия, игнорирующая маловероятные пути по решетке, как только они становятся маловероятными. Стратегия поиска на решетке только наиболее вероятных путей известна под общим названием последовательных алгоритмов. Как правило, в последовательных алгоритмах не принимается окончательных решений о непрерывном отбрасывании путей. Время от времени последовательный алгоритм принимает решение вер- нуться обратно и продолжить оставленный ранее путь. Последо- нательные алгоритмы в равной мере пригодны и для поиска по дереву, и для поиска по решетке.

Представим себе решетку с большой длиной кодового ограни-; чения, скажем, равного 40. Для принятия первого решения в та-, кой решетке надо обработать несколько сотен кадров. Каждый кадр содержит и вовсе огромное число вершин, а именно 2 , или, примерно, Ю вершин. Последовательный алгоритм должен найти наиболее близкий к заданной последовательности путь на этой решетке; он должен сделать это, по крайней мере, с очень высокой вероятностью, хотя время от времени ему дозволено отказаться от декодирования. Этот отказ связан не с недостаточностью данных, а с неполнотой алгоритма. В алгоритме Витерби мы не встречались с ошибками подобного сорта.

Последовательный алгоритм просматривает только первый, кадр, принимает решение и переходит в вершину решетки перво: уровня. Затем он повторяет эту процедуру. На каждом уровне,; находясь только в одной вершине, он просматривает следующие; кадр, выбирая ребро, ближайшее к принятому кадру, и nepexo-j дит в вершину следующего уровня, прокладывая таким образ!

путь на дереве. Если заданная последовательность точно совпадает с некоторы.м путем на дереве, то эта процедура работает хорошо. Однако при наличии несовпадений последовательный алгоритм выбирает иногда неправи.тьный путь. Если алгоритм продолжает следовать по ложному пути, он внезапно обнаружит, что в каждом кадре расходимость слишком велика и, по-внди.мо.му, он на неправильном пути. Последовательный алгоритм вернется назад на несколько кадров и начнет исследовать альтернативные пути до тех пор, пока не найдется правдоподобный путь. Затем он будет двигаться вдо.ть этого альтернативного пути. Ниже будут кратко описаны правила, которыми он руководствуется при этом поиске.

Характеристики алгоритма зависят от ширины b окна. Если алгоритм нашел путь, проходящий через b кадров дерева, он принимает окончательное решение относительно самого старого кадра, выводит этот кадр и вдвигает в окно новый кадр.

Число вычислений, необходимое последовательному алгоритму для продвижения по дереву иа одну вершину вглубь, является случайной величиной. Эта величина служит основной характеристикой последовательного алгоритма. Она представляет собой основной параметр, определяющий сложность алгоритма, необходимую для обеспечения заданного уровня его .характеристик. Если помехи малы, то алгоритм ножет двигаться по правильному пути, используя для продвижения вглубь по дереву на одну вершину только по одному вычислению в каждом кадре. Но если имеются сбивающие помехи, то алгоритм может пойти по неправильному пути, что приводит к задержке и большому числу вычислений, предшествующих выходу на правильный путь. Переменность числа вычислений влечет за собой необходимость большого объема памяти для входных данных. Любой буфер конечного объема, независимо от его величины, при использовании в последовательном алгоритме имеет ненулевую вероятность переполнения. Такое поведение а.тгоритма следует рассматривать как одну из его характеристик. Переполнение буферной памяти является существенным фактором любого алгоритма, который осуществляет по меньшей мере одно вычисление в каждой посещаемой вершине и который последовательно просматривает ребра так, что записанные на более глубоких ребрах дерева данпые не используются. Второе условие оказывается критическим и приводит к особому поведению алгоритма.

Испо.тьзуемые последовательные алгоритмы разбиваются иа два класса: стек-алгоритм, рассматриваемый в настоящем разделе, и алгоритм Фано, который будет рассмотрен в следующем разделе. Структура их совершенно различна. Используемые в этих двух подходах метрики являются предметом непрерывных обсуждений. Необходимое число вычислений в стек-алгоритме меньше.

Начаугьное состояние: стек начинается с единственного пути dJuHbi нуль

Продолжить пути из вершины стека в

успешных Seputuj\ Дополнить метрику до метрики каждого нового пути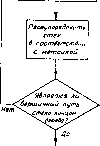

Стоп

-Выдать вершинный путь стека

Рис. ритм.

12.9. Упрощенный

Расходимость пути определяется как логарифмическая функция правдоподобия этого пути и вычисляется следующим образом. Первые N -- 1 кадров заданного слова можно записать в виде

v = W.....С 1, v4\ -ок).

Первые т -f 1. кадров символов вдоль произвольного пути можно записать в виде

с - (с1.....с;-, с\.....с?-..... .....сУ).

Мы хотим отыскать отрезок пути на дереве, который максимизирует Рг (с* I v ). Последовательный алгоритм выбирает начальный отрезок пути по дереву, не заглядывая в глубь дерева. По правилу Байеса,

> Рг(у1 ))

Член Рг (vC) I с< 4) можно разбить на два множителя

П npr( ici)

го 1-1

п npr(fO

,- m+! /-1

Первый член равен произведению условных вероятностей для m + 1 кадров истинного пути; второй множитель равен произведению безусловных вероятностей по тем кадрам, где путь не определен. Это разложение является следствием определения последовательного алгоритма. Алгоритм более общего вида не обязательно допускает такое разбиение.

Теперь будем максимизировать вдоль путей величину

Рг (у1>с )Рг(с ) Prlv )

П П Vr(v[\c{) 1=0 ;-1

П Й Рг {v{)

Рг(с< 4),

Так как все пути предполагаются равновероятными, то член Рг (с1 >) является константой. Его можно отбросить, и это не влияет на выбор максимума. Используемая в рассматриваемом последовательном алгоритме метрика, именуемая метрикой Фано, задается логарифмической функцией

г Pr(v U )Pr(c° ) р (cl )) = log, Pr(v< >)

-1 2

I чем в алгоритме Фано. Стек!

алгоритм запоминает уже вы- численный набор путей. Это контрастирует с поведением алгоритма Фано, который, найдя свой путь в некоторук вершину, может вернуться на какое-то расстояние обратно только для того, чтобы повторить во всех деталях путь в ту же вершину. Стек-алгоритм предпочитает запоминать проделанную работу, а не повторять ее, С другой стороны, для стек-алгоритма требуется существенно больший объем памяти и большая вычислительная работа на каждой итерации.

Стек-алгоритм легок для; понимания; его упрощенная блок-схема приведена на рис. 12.9. Алгоритм организуется вокруг стека уже вы- численных на предыдущих! итерациях путей различной-длины. Каж.вдй вход в стек представляет собой путь, они-, сываемый тремя величинами! длиной пути; последователь- ностью переменной длины, со- держащей определившие данный путь переходы между состояниями; и расходимостью данного пути. В начальный, момент стек содержит только! тривиальный путь нулевой} длины.

Расходимость пути определяется как расстояние между сегмен-! том пути и начальным сегментом данных той же самой длины.! Используемые в последовательных алгоритмах расстояния изме-С ряются многими разными способами. Во многих важных задачах! последовательность данных представляет собой последователь-! ность записанных на ребрах символов, искаженных аддитивным-! шумом. В этом случае мера расстояния известна как мгтрикф\ Фано, которая сейчас будет определена.