Машина с конечным числом состояний, производяш,ая в каждый момент времени один или более элементов некоторого поля F, генерирует последовательность элементов этого поля. Множество всех возможных таких последовательностей на выходе машины с конечным числом состояний описываются графом определенного вида, который называется решеткой или, в случае очень большого числа состояний, деревом. Имеется много приложений, в которых по результатам наблюдений в шуме одной из таких последовательностей требуется оценить либо .саму эту последовательность, либо историю машины с конечным числом состояний. Это задача поиска по решетке или по дереву такого пути, который лучше всего отвечает данной последовательности. Такое направление в обработке дискретных сигналов сильно отличается от других направлений, и алгоритмы, рассматриваемые в настоящей главе, сильно отличаются от уже изученных нами алгоритмов.

Алгоритмы поиска по решетке и по дереву находят приложения в таких областях, как декодирование сверточных кодов, демодуляция сигналов при наличии межсимвольной интерференции, демодуляция сигнала по частичному отклику или фазово-разностно-модулированных сигналов, распознавание речи и текстовых символов.

12.1. Поиск по решетке и по дереву

Решетки и деревья, по которым реализуется поиск, возникают как описания машин с конечным числом состояний. Машина с конечным числом состояний задается множеством состояний, в которых она может находиться, множеством переходов между этими состояниями и выходными символами, соответствующими каждому такому переходу. Простейший способ построения машины с конечным числом состояний с помеченными переходами состоит в использовании регистра сдвига так, как показано на примере на рис. 12.1. Состояния машины в этом примере описываются двумя содержащимися в ячейках регистра сдвига битами; всего имеется четыре так определяемых состояния. В каждый момент времени на вход поступают два бита, так что из каждого состояния возможны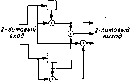

rtTu

tn zZ -д-

Рис. 12.1 Пример машины с конечным числом состояний,

3 модулю 2 (НС-

Рис. 12.2. Другой пример маши1[ы с конечным числом состояний. 4- обозначает сложение по модулю 2 (исключающее ИЛИ)

четыре перехода. В данном частном примере из каждого состояния возможен прямой переход в любое другое состояние. Изображенная на рис. 12.1 схема имеет три выходных бита; каждый переход порождает трехбитовую последовательность.

На рис. 12.2 показан другой пример, в котором уже нельзя из произвольного состояния перейти в любое другое состояние. Для достижения некоторых состояний требуется совершить два перехода. Схема на рис, 12.2 имеет двухбитовый выход.

Диаграмма переходов для машины с конечным числом состояний показана на рис. 12.3. Переходы помечены векторами длины два. В каждый .момент времени машина делает переход между состояниями вдоль пути и метит путь переходов. Приведенная на рис. 12.3 диаграмма соответствует схеме на рис. 12.2.

Как правило, вид графа, который называется решеткой, можно использовать для описания выходных последовательностей произвольной машины с конечным числом состояний. Типичная решетка, из каждой вершины которой выходят два ребра, показана на рис. 12,4. Вершины любого столбца решетки обозначают состояния, в которых может находиться машина. Каждый последовательный столбец соответствует последовательным моментам времени и содержит одно и то же множество состояний. Ребра, связывающие вершины двух столбцов, представляют собой все возможные переходы в течение данного временного интервала, именуемого кадром. В общем случае решетка представляет собой полубесконечный вправо прямоугольный граф, число вершин в каждом столбце которого конечно. Расположение ребер, связывающих вершины данного столбца с вершинами следующего справа столбца, одно и то же для каждого столбца. Диаграмма начинается в верхней левой вершине; так как движение осуществляется только вправо, то недостижимые левые узлы на диаграмме не указываются. Длиной кодового ограничения решетки называется число битов, необходимых для определения состояния на решетке. Длина кодового ограничения решетки, показанной на рис. 12.4, равна двум.

БЫСТРЫЕ АЛГОРИТМЫ ПОИСКА ПО РЕШЕТКЕ и по ДЕРЕВУ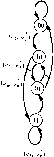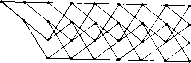

(.., Го соя 1; р п-- .

Каждый кадр машины с конечным числом состояний приводит к изменению состояния. На решетке это изменение показано реб- ром, входящим в с.тедующую вершину. Каждое ребро на рис. 12.5 помечено. В общем случае ребро маркируется некоторым фиксированным числом По элементов основного поля F. При переходе от кадра к кадру множество меток на ребре может быть как фиксированным, так и переменным. Машина с конечным числом состояний может двт(гаться по решетке слева направо по многим путям решетки. Идя по каждому из этих путей, она вычисляет некоторую последовательность элементов поля F, которая и является ее выходной последовательностью.

Пусть с = Cj, i = О, ...j обозначает последовательность символов источника над полем F, генерируемых машиной с конечным числом состояний, и пусть V = \v i = О, ...) обозначает последовательность символов данных над F. Во многих приложениях Vi = Ci + e-i, где е, - составляющая ошибки. О такой ситуации говорят, что последовательность на выходе источника наблюдается в аддитивном шуме.

Задача поиска по решетке состоит н вычислении такого пути на решетке, для которого последовательность с согласуется с заданной последовательностью v данных наилучшим образом. Для из- , мерения меры согласованности необходимо ввести функцию расстояния.

Расстояние на множестве S определяется как вещественная функция(а, Р) на паре элементов из 5, удовлетворяющая условиям

1. d (а, Р) > О и d (ос, а) = 0.

2, d (а, Р) = d ф. а).

Если эта функция удовлетворяет также условию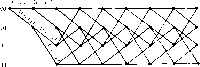

Рис. 12.5. Маркированная решетка.

3. d (а, РХ d (а, у) + d{y, Р) для всех у из S, то она называется метрикой. Евклидово расстояние, определяемое на л-мерном векторном пространстве формулой

d(v, w)

является метрикой. Каждый состоящий из / кадров путь на- решетке определяет вектор длины In над полем F. Если из каждой вершины решетки выходит q путей, то на длине путей в / кадров мы получаем q таких векторов длины Iuq. Задача поиска по решетке состоит в выделении того из этих векторов, который ближе всего в данном расстоянии подходит к данному вектору v длины triq.

Наиболее простой для понимания метод поиска по решетке состоит в вычислении всех расстояний данного вектора v от последовательностей, производимых данной решеткой, и нахождении в полученном списке наименьшего расстояния. Это можно проделать, мысленно накладывая заданную последовательность v на каждый из возможных путей на решетке. Сложность этой процедуры растет экспоненциально по /, так что при больших I она практически неприемлема. Обычно / столь велико, что его можно полагать бесконечным. Практически алгоритм не может рассматривать всю входную последовательность целиком при больших I. Он начинает с самого начала и, двигаясь вдоль последовательности, принимает окончательные решения. Эффективный поиск по решетке можно осуществлять по алгоритму Витерби, который будет описан в следующем разделе.

В некоторых случаях число состояний машины с конечным числом состояний велико. Тогда число узлов в каждом кадре решетки также велико, иногда настолько, что его можно полагать неограниченным. В этом случае исходная часть решетки тоже растет неограниченно, и в графе мы пренебрегаем тем, что на самом деле при возврате машины с конечным числом состояний в некоторое состояние в конечном итоге пути рекомбинируют. Ведь в каждый момент времени приходится рассматривать лишь малые фрагменты решетки. Хорошим изображением того, что происходит.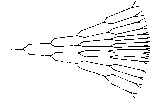

Рис. 12.5. Дерево с двумя ребрами в каждом узле.

является представленное на рис. 12.6 дерево. Число узлов дерева растет неограниченно.

Так же как на решетке, / кадров маркированного дерева определяют векторов. Задача поиска по дереву состоит в нахождении того из этих векторов, который ближе всего к заданному вектору v данных. Мы можем мысленно наложить данную последовательность на кйждый из возможных путей дерева длиной в 1 кадров и определить наилучшее совпадение. Опять сложность этой процедуры растет экспоненциально по /. так что практичесиг она неприемлема. Эфс{)ектионые процедуры поиска по дереву даются последовательными алгоритмами, рассматриваемыми в следую-п!.их параграфах,

12.2. Алгоритм Витерби

Принцип оптималыюсти динамического программирования утверждает, что если в некотором смысле оптимальный путь от точки А к точке С проходит через точку В, то отрезок пути из точки В в точку С совпадает с оптимальным путем из точки В в точку С. Этот принцип применим к задаче отыскания лучшего пути по решетке. Основанная на этом принципе итеративная процедура построения переменного множества претендентов на лучший путь по решетке известна под названием алгоритма Витерби,

Алгоритм Витерби для решетки с q ребрами в каждой вершине и длиной кодового ограничения v оперирует претендентами, так что его сложность пропорциональна q. Практически алгоритм пригоден только прп малых v. Если длина кодового ограничения равна 10 и из каждой вершины решетки выходят два ребра, то алгоритм Витерби оперирует 1024 претендентами. Практически это допустимо. Но при длине кодового ограничения 20 число претендентов уже больше миллиона, так что алгоритм практически неприемлем.

Двигаясь вдоль решетки, алгоритм Витерби итеративно обрабатывает кадр за кадром. Находясь на некотором кадре в момент /,

алгоритм не знает, какая из вершин является ближайшей, и даже не пытается вычислить эту вершину. Вместо этого алгоритм определяет лучший из путей от начальной вершины до каждой из вершин /-Г0 кадра. Он вычисляет расстояния между данной последовательностью и всеми претендентами для каждой вершины /-го кадра. Для каждого из путей-претендентов это расстояние называется его расходимостью. Если все пути-претенденты проходят в первом кадре через одну и ту же вершину, алгоритм находит первый кадр ближайшего пути, но не принимает при этом никакого решения относительно /-го кадра.

Далее алгоритм вычисляет пути-претенденты в каждую новую вершину (/ + 1)-го кадра. Но чтобы попасть в любую новую вершину (/ + 1)-го кадра, путь должен пройти через одну из старых вершин /-Г0 кадра. Таким образом, пути-претенденты в новые вершины можно получить продолжением старых претендентов, которые допускают такое продолжение. Ближайший путь вычисляется прибавлением прираш,ений расходимости каждого пути к расходимости лучшего пути в старую вершину. В каждую новую вершину ведут путей, и путь к новой вершине с минимальным приращением является ближайшим. Этот процесс повторяется для каждой из новых вершин. В конце вычислений, связанных с новым кадром, алгоритм вычисляет ближайший путь в каждую из вершин этого кадра / + I. Если опять все эти пути проходят через одну и ту же вершину второго кадра, то алгоритм Витерби успешно вы,-числяет второй кадр.

Этот процесс повторяется во всех успешных кадрах. Если в некоторый момент возникает несколько ближайших путей в данную вершину, то алгоритм должен разрешить этот конфликт, используя некоторое правило. Альтернатива состоит в сохранении всех решений, так что, например, находятся два пути в данную вершину. Для лучшего понимания этого момента следует обратиться к рассматриваемому ниже примеру.

Для реализации алгоритма Витерби надо выбрать окно ширины Ь, которое, как правило, в несколько раз превышает ширину кодового ограничения v и диктуется возможностями используемого компьютера. В момент п алгоритм просматривает все выжившие пути. Если в первом кадре они совпадают, то этот кадр выбирается в качестве первого кадра правильного пути; его можно передать пользователю.

Далее алгоритм отбрасывает первое ребро и переходит к вычислению следующей итерации, беря для этого новый кадр. Если опять все выжившие пути проходят через одну и ту же вершину наиболее старого кадра, то этот кадр принимается. Этот процесс повторяется бесконечно, вычисляя кадр за кадром.

Если b выбрано достаточно большим, то в данном кадре почти всегда можно принять однозначное решение. Редко, но ветре-