берлвкзмпо -Мвсса

Six) = F {x) t Г {лг)

ESS I

Рис. 11.7. Разложение алгоритма Рис. 11,8. Рекурсивный алгоритм Бер-Берлекэмпа-Месси. лекэмпа-.Месси. -

Это завершает описание разбиения алгоритма Берлекэмпа-Месси Основная форма алгоритма теперь записывается в виде

1 -

где вместо (х) подставляется F* (.v) или Fii (х), а вектор ( 1 (х), Я2 (х)) в первой половине вычислений равен (а (х), а (х)), а во второй половине вычислений модифицируется в вектор а -(х). После того, как вычислены обе половины задачи, ма-. трица F( l (х) получается перемножением своих двух половин.

Разбиение алгоритма Берлекэмпа-Месси показано на рис. 11.7. Заметим, что каждая из половин а.чгоритма сама является алгоритмом Берлекэмпа-Месси. Следовательно, если п/2 четно, то каждая из половин может быть разбита в свою очередь: если п равно степени двух, то такое разбиение можно продолжить до тех пор, пока ке будут получены фрагменты, состоящие только из одной итерэ-

иии в этих фрагментах выполняются уже все вычисления, но они достаточно тривиальны.

На рис. 11.8 алгоритма приведена рекурсивная форма Берлекэмпа-Месси. Вся вычислительная работа сводится к вычислению полиномиальных произведений, сочетающих половинные результаты. Эти вычисления представляют собой свертки многочленов и могут быть выполнены с помощью любого алгоритма линейной свертки.

11.5. Методы, основанные на алгоритме Евклида

В некоторых методах решения теплицевых систем уравнений используется алгоритм Евклида. Наиболее подходящей для этого является описанная в разд, 10.7 рекурсивная форма алгоритма Евклида.

Начнем со следующей теплицевой системы уравнений;

Это та же самая теплицева система уравнений, которую в § 11.3 мы решали с помощью алгоритма Берлекэмпа-Месси. Пусть

а(х)= Ё а,х, l(x) = l + tfiX,

/=о (=1

я рассмотрим произведение этих многочленов g (х) = (х) а (х). Из выписанного матричного уравнения видно, что

gi = О, i = п.....2л - 1,

но при значениях индекса (, больших чем 2п - 1, коэффициенты g, могут быть и ненулевыми. Рассмотрим задачу вычисления таких / (-V) и g (х), которые удовлетворяют условиям deg / (х) .< л, fl2g g (х) < л - 1 и

g (х) = / (х) а (х) (mod х ).

Одним нз путей решения этой задачи, конечно, является решение исходного матричного уравнения относительно вектора f и дальнейшего вычисления многочлена g (х). Другой метод основан на использовании алгоритма Евклида для многочленов.

Для того, чтобы увидеть, как можно решать это уравнение относительно / (х) и g (х), вернемся к доказательству алгоритма

s(x) t{x)

t{x) = A!S(x)t{x} (modsW),

что при t (х) - а (х) и S (х) = х- является одной из форм решае- i мого нами уравнения. Выписанное уравнение справедливо при] всех г. Чтобы решить задачу, надо найти такое г, при котором \ deg Лр (х) < я и deg (х) < - 1. Если такое г существует, ; то многочлены ЛЁ (х) и ( (х) должны равняться искомым мно- гочленам / (х) ч g (х). Выберем значение г, при котором удовлетво-; ряются неравенства

deg(<-4(x)>n и deg(()(xXn- 1.

Так как deg ((о (х) = 2п и с ростом г степень многочленов ( > (х) строго убывает, то это определяет г однозначно. При таком опре- ] делении г требование deg t<> (х) < я - 1 у.човлетворено. С ростом г степень многочлена ,422 (х) растет, и надо только показать, , что deg Ли (х) < п. Для того, чтобы это доказать, воспользуемся матрицей, обратной к матрице А (х). Сначала напомним, что

ГО 1

А<1 (х) = П

1 -Qi x)

eg Л2: (х) > deg Ли (х). Напомним также, ; t > (х). Из этих неравенств и матричного

Отсюда ясно, что что deg s<> (х) > dl уравнения

- А;, (X) Л,1 (x)J I

leg ЛЙ W + deg sМ. к так как sf> (х) = (х), то это преобразуется к соотношению

deg ЛЙ (х) = degs (X) ~ deg t (х)< 2я - я = я,

sM(x) tin (X)

следует, что

где неравенство вытекает из определения параметра г.

Мы получили почти полное доказательство следующей теоремы.

Теорема 11.5.1. При заданных s l (х) = х и Г( > (х) = а (х) пусть

А< ) (X) =

I О О 1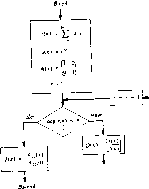

Рис. 11.9. Решение теплицевой системы с помощью алгоритма Евклида.

Продолжая рекурсию до тех пор: пока deg (<Чх) <п- \, решим следуюш,ую систему рекуррентных уравнении:

АС-ч (X), s<-44x)

[1 -Q<>WJ О 1

.1 -Q< W

и положим g (х) = Д / (х) и / (х) = Д-ЛЙ W, где А = = Ли (0). При условии, что Д отлично от нуля, эти многочлены удовлетворяют уравнению

g (х) = f (х) а (х) (mod х ).

причем deg / (х) < п, deg Г < я - 1 /о = 1

Доказательство. Деление на Д обеспечивает равенство f = \. Справедливость остальных утверждений была установлена ранее. Q

Евклида. Из этого доказательства легко увидеть, что

Г .:

Задачи

Используя алгоритм Левинсона, решить Б поле GF (7) уравнение

И.2. Реконструировать алгоритм Левинсона для случая, когда основное поле является комплексным, а матрица А эрмитовой.

11.3. Предположим, что влодящая в ajffopifTM Берлекэмпа последовательность а является периодической, период которой намного больше, чем 2п,

а. Показать, как можно полностью вычислить последовательность по ее первым 2п компонентам.

б. Предположим, что вместо вектора а задано его преобразование Фурье, вектор А. Показать, как надо модифицировать алгоритм Берлекэмпа - Месси для того, чтобы использовать непосредственно вектор А, не вычисляя обратного преобразования Фурье.

11.4. Используя алгоритм Берлекэмпа - Месси для входной последовательности (Оо, Oj., 07) = (О, О, О, О, О, О, О, 1). найтн решение i, длина которого больше 4. Эта задача является примером того, как алгоритм Берлекэмпа - Месси приводит к авторегрессионному фильтру даже в тех случаях, когда теплицева матрица вырождена.

11.5. Используя алгоритм Евклида, решить уравнение

11.6. Доказать, что все шаги рекурсии алгоритма Левинсона можно провести в том и только Б том случае, когда все вложенные главные подматрицы невырождены.

1 1.7. Сформулировать условия невырожденности алгоритма Дурбина.

Замечания

Первый быстрый алгоритм решения теплицевых систем уравнений был раз-ан Левинсоком (1947). Он был сразу же откеген скорее к области приложений к задачам вннеровской фильтрации, чем к задачам построения быстрых алгоритмов как таковых. Другие быстрые алгоритмы решения некоторых теплицевых систем уравнений были построены Дурбиным (1960), Тренчем (1964) и Берле-кэмпом (1968), Упрощение алгоритма Тренча предложил Зонар (1974). Месси (1969) упростил алгоритм Берлекэмпа, интерпретируя его как метод построения регистра сдвига с линейной обратной связью. Вслч и Шольц (1979) списали этот же алгоритм с точки зрення алгоритма построения непрерывной дроби. Рекурсивную форму алгоритма Берлекэмпа - i4eccH описал Блейхут (1983). Использование алгоритма Евклида для решения теплицевых систем уравнений предложено Сугиямой, Касахарой, Хирасавой и Намекавой (1975). Ускорение алгоритма Евклида с помощью дублирования в его приложении к решению теплицевых систем уравнений разработали Брент, Густавсон и Юн (1980).

Неудивительно, что быстрые алгоритмы решения теплицевых систем уравнений связаны со многими другими задачами. Если выписать шаги алгоритма Левинсона в обратном порядке, то он преобразуется в алгоритм, известный как критерий Шура - Коена для тестирования стабильности аБторегрессион1Юго фильтра, задаваемого многочленом а (х). Эту связь отметнлк Вийера и Кайлат (1977),

Объем КИНГИ немедленно бы удвоился, если бы мы стали рассматривать такие обобщения н специализации теплицевых матриц, как блочно-теплицевы матрицы или почти теплицевы матрицы. К таким работам относятся статьи Виг-гинса и Робинсона (1965), Днкинсона (1979). Днкинсонз, Морфа и Кайлзта (1974), Фридлендеря, Морфа, Кайлата и Льюнга (1979). Морфа, Дикинсона, Кайлата и Байеры (1977), Мондена и Аримото (1980).

Таким образом, .мы получили другой способ решения той же самой теплицевой системы уравнений (в случае, когда эта система обратима), которую мы уже решали раньше, используя алгоритм Берлекэмпа-Месси; - блок-схема этого метода показана на рис. 11.9. Если теплицева система не обратима, то описанное применение алгоритма Евклида также приводит к многочлену ,4;;;) (х) наименьшей степени, который удовлетворяет определяющему его равенству, но а этом случае Д = О и поэтому многочлен f ix) не определен. Если Д = О, то описанный алгоритм приводит к решению системы