сдвига с требуемым свойством. Прежде, чем доказывать эту теорему, получим границу для длины регистра сдвига.

Теорема 11.3.1. Пусть (х)) - регистр сдвига с ли-

нейной обратной связью минимальной длины, генерирующий последовательность Ol, а,, а (ir, /* (х)) - регистр сдвига с линейной обратной связью минимальной длины, генерирующий по-, следователь ность а, а, и f- (х) ф f-(х). Тогда;

ii > max г - Lr.i I.

Доказательство. Неравенство, которое требуется доказать, разбивается на два неравенства

> Lr-.i и L, > г -Первое неравенство очевидно, поскольку если регистр сдвига с линейной обратной связью генерирует некоторую последовательность, то он генерирует и любую меньшую последовательность, являющуюся началом исходной. Если > г, то второе неравен- j ство также становится очевидным. Поэтому предположим, что > U-i < г и второе неравенство не выполняется, и попытаемся . прийти к противоречию. Из предположения следует, что < . <: г - 1 - Lr 1- Для сокращения записи введем временные обо- значения: с (х) = fi- (х), Ь (х) = f<i (х), L = и L = L,. В новых обозначениях исходные предпо.тоження принимают вид: L < г ч г L + V + 1. Кроме того, из условий теоремы следует, что

Oj = - £ Ьф , j = L + 1, .... г.

Теперь установим противоречие. С одной стороны,

а, = - S lir-h = S S Сгйг-.*-,-, 11=1 t=i (=1

где справедливость разложения Q-h следует из того, что г - к пробегает целые значения от г - 1 до г - L, содержащиеся среди чисел L -t- 1, ...,г - 1, в силу предположения г L ~ L + I. С другой стороны,

L Li

1 = 1 (=! fe>l

11.3. Алгоритм Берлекэмпа-Месси

где справедливость разложения следует из того, что г - j

пробегает содержащиеся среди чисел L -г 1, г - 1 целые значения от г - 1 до г - L, а это, в свою очередь, следует из предположения г > L -- L + I. Изменение порядка суммирования в правой части последнего равенства приводит к выражению для а полученному в правой части предыдущего равенства. Таким образом, получаем доказывающее теорему противоречие а ф фа. и

Если удастся построить регистр сдвига с длиной, удовлетворяющей соотношению из теоремы 11.3.1 с заменой знака нестрогого-.неравенства знаком равенства, то тем самым будет построен регистр сдвига минимальной длины. Доказательство теоремы 11.3.2 предъявляет конструкцию такого регистра сдвига.

Теорема 11.3.2. Предположим, что {L /< (.х)), i= 1, ...,г, является последовательностью регистров сдвига минимальной длины с линейной обратной связью, таких, что (Ь /<) (х)) генерирует последовательность а, Uj. Если /<> (х) Ф ff-->> (х), то

Lr = max (Lr г - L, i]

и любой регистр сдвига, генерирующий а, а, и имеющий длину, совпадающую с величиной правой части последнего равенства, является регистром сдвига минимальной длины.

Доказательство. Согласно теореме 11.3.1 не может быть меньше величины в правой части последнего равенства. Если удастся построить какой-либо регистр сдвига, который генерирует требуемую последовательность и длина которого совпадает с указанной величиной, то он будет регистром сдвига минимальной длины. Доказательство будет проводиться по индукции. Мы построим удовлетворяющий теореме регистр сдвига в предположении, что такие регистры последовательно построены для всех < г - 1.

Для йаждого к, к = 1.....г - 1, обозначим через (Lj, f(х))

регистр сдвига минимальной длины, генерирующий а.....а .

Примем за предположение индукции, что

ift = шах* - Lft.il, k=\, ....r-\,

каждый раз, когда / > (х) ф /<*-ii (х). Это, очевидно, верно для А = О, если Ui отличен от нуля, поскольку /-о = О и = 1. В более общем случае, если а - первый ненулевой элемент в заданной последовательности, то L, i = О и i, = i. Тогда предположение индукции относится к индексу к = i.

Значение к в последней итерации, приведшей к изменению длины, будем обозначать через т. Последнее означает, что при завершении (г - 1)-й итерации m является целым числом, таким, что

392 Гл. U. Быстрые методы решения теплицевых систем Теперь имеет место следующее равенство:

i-r-i -,-1 О, / = .....r-l,

(=1 i=o 1, г. ; - f I

Если Д,. = О, то регистр (/ ], /< -I {х)) также генерирует пер- Bbje г символов, и, таким образом,

ir = ir-i и /<)(х) = /(- (х). Если ф О, то необходимо построить новый регистр сдвига, Напомним, что изменение длины регистра сдвига произошло прн k = т. Следовательно,

и по предложению индукции

= = max [im-i. m - im-ll = m - m-l. поскольку L > Теперь выберем новый многочлен

/ (х)=/ - (х)-Д,Д;;х-°/< (х:) - 1

и положим = deg /<> (х). В этон случае поскольку deg f<-4 (х) < L, i и deg [х- / -! (х) 1 < г - m + L i, то

Lr < max г - m L ,l < шах [Lj, r - Lr-il-Из теоремы II.3.1 при условии, что (L, f(х)) генерирует Й1, Or, следует, что Л, = шах IZ-r-i. г - L, i\. Осталось только доказать, что регистр сдвига (L /о (х)) генерирует требуемую последовательность. Докажем это непосредственным вычислением разности между и сигналом на выходе обратной связи регистра сдвига;

\ (=1 /

- Д,Д

О i = U,L,+ l.....г-1,

. Д, - Д,Д;Д = 0,)=г. Итак, регистр (L / > (х)) генерирует а, а,. В частности, (i-n, / (х)) генерирует а й и теорема доказана. О

Теорема 11.3.3 (Алгоритм Берлекэмпа - Месси]. Пусть заданы .....а из некоторого поля, и пусть при начальных условиях (х) = 1, и°1 (х) =1 и io = О выполняются следующие

рекуррентные равнства, ucnoj зуемые для вычисления (х);

7 > (хУ (х).

1 - Дг

д;6, (1 -6,)х

р- (х)

((-1) (X)

г 1, 2п, где 6 - 1, еси одновременно А ф О и 2Lr i < г - 1, W bj. = Q в противном случае. Тогда (х) является многочленом наименьшей степени, коэффициенты которого удовле- -творяют равенствам /( > ~ \ и

r=Lor-\, 2г.

Доказательство. Следует из теоремы 11.3.2. □

В этой теореме может обращаться в нуль, но только в том случае, когда 6;. = 0. Положим тогда по определению Дб/- = 0.

Блок-схема алгоритма Берлекэмпа-Месси приведена на рис. 11.6. На г-м шаге указанный алгорит.м содержит число умножений, равное примерно удвоенной степени многочлена f* (х). Степень многочлена {х) равна примерно г/2, и всего имеется 2п итераций, так что всего алгоритм содержит примерно

2п = умножений и примерно такое же число сложений. Ко-роче можно сказать, что порядок числа умножений в алгоритме Берлекэмпа-Месси равен п, илн, формально, О (/г).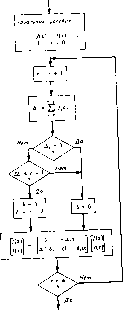

Рис, 11.6. па-Месси.

Crnoi

Алгоритм Берлек.м-

F (x) =

F\l(x) F\%x) F ix) fS(x)

Коэффициенты многочлена F\i (x) будем обозначать через fiy.t. Матрица F<> (х) определяется так, чтобы многочлены (х) и (х) можно было вычислить, используя уравнения

Напомним, что сначала выполняемые в алгоритме Берлекэмпа- Месси вычисления записываются в виде двух уравнений:

Г/ >(х)1 г Чх)

1 -Л,х Д,-6, (1 - S,)Xj

/ - (х) (- (х)

1 -А,х 1 1 -i,x

Д;6, (1 - S>J дг6, (1 -Ь,)х.

Следовательно,

г =

Алгоритм модифицирует как матрицу F ) (х), так и многочлены /о (х) и (О (х). Прямой метод перевычисления F* (х) требует примерно в два раза больше умножений, поскольку матрица содержит не два элемента, а четыре. Хотя в такой форме вычисления и допускают использование метода дублирования, но мы получаем большее, чем хотим, число умножений. Надо соответствующим образом реорганизовать вычисления.

Рекурсивная форма алгоритма Берлекэмпа-Месси строится вокруг следующих уравнений, эквивалентных выписанным ранее:

Предполагая п четным, разобьем алгоритм пополам и положим F< > (.V) .= Р- 1 .1(х)Г 1 )(х),

F(->W.

п12+\ f (1) (х) = П

Р- < /2> (Х) == П

Г=п 2

&;% (l-e,)xj 1 - Д,х

.....АГ6, (l-6,)xj

Мы будем вычислять каждую из половин отдельно, а затем их перемножать. Сложность при этом получается меньше, чем в исходном способе решения. Необходимо также реорганизовать уравнение, определяющее Д. Будем величину Д, вычислять как г-й коэффициент первой компоненты двумерного вектора многочленов (.V) F[r\x)\\a(x) а{х)

Таким образом, для г, больших чем )i,/2.

Д(х)

= F4->()F W

а(х) а(х)

= Fi-i>(x)a( -> (х).

а< =1 (X) = Р < 2> (х)

а{х) 1а{х)

11.4.Рекурсивный алгоритм Берлекэмпа-Месси

Все рассмотренные нами до сих пор методы решения теплицевых систем уравнений содержат число умножений, пропорциональное rt. В настоящем параграфе мы воспользуемся стратегией дублирования для того, чтобы снизить вычислительную сложность алгоритма Берлекэмпа - Месси при больших п.

Число используемых на г-м шаге итераций умножений примерно равно удвоенной степени многочлена /<> (х). На первых шагах итераций эта степень мала, и итерации выполняются легко, но с ростом г растет и сложность вычислений. В ускоренном алгоритме за счет одновременного выполнения нескольких итераций используется преимущество, которое дается простотой вычислений на первых шагах. После выполнения каждой такой группы итераций исходная задача модифицируется так, чтобы учесть это полученное решение. Затем сызнова начинается выполнение новой группы итераций алгоритма Берлекэмпа-Месси, но уже для модифицированной задачи и модифицированного начального значения многочлена / (х).

Рассматриваемое ниже построение начинается с более компактной организации алгоритма Верлекэмпа-Месси. Заменим многочлены / (х) и t<> (х) полиномиальной матрицей размера 2x2: