ILJ±2LI!Ptj;:;P >< плицевых систем

Вход В вАгаритм Тренча

Начальные условия

г= О

С. = Нулебои вектор с- = Нулевой вектор

Рис. И.З. Алгоритм Тренча.

номы уто его воспользовавшись равенством Ь!Г- ° ° -1- Тогда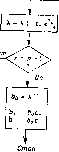

тГеГ;Гс74 с:ГГ-формулировку теореш.. горитматрча. ВсТчто осталось сделГвоГ ФРР определеник, обозначение, ярГкГрЧГвГчГи

11,3 .Алгоритм Берлекэмпа-iHeccn

руемые символом г, стоят в левых частях рекуррентных уравнений, азе.нчины, индексируемые символом г - 1, стоят в правой части.

.Алгоритм Тренча подытожен на рис. 11.3. Блок-схема основана на геореме И.2.4, но величины Ь., Ь и в итерациях заменены нормализованными величинами с+, с и в соответствии с равенствами

-bi: и я< =

Соответственно рекурсия описывается уравнениями

L 1 J

L 1 J

X = x - (i- c;c: ) -Ha рис. 11.3 использована эта форма уравнений.

11.3. Алгоритм Берлекэмпа-Месси

Алгоритм Берлекэмпа-Месси представляет собой алгоршт цення в произвольном поле F теплицевой системы уравнений

реше вида )

.Матрица системы не является симметрической, что требуется для применимости алгоритма Левинсона. С другой стороны, стоящий в правой части системы вектор не является произвольным, а составлен из компонент матрицы системы.

Лучшим подходом к алгоритму Берлекэмпа-Месси является интерпретация выписанного матричного уравнения как описания авторегрессионного фильтра. Предположим, что вектор f известен. Тогда первая строка рассматриваемого матричного уравнения определяет а через а , а, .... вторая строка определяет a .i

через 1.....а , и т. д. Этот последовательный процесс описывается

уравнением

= - S fij-f i = л. (=1

2л- 1.

) в настоящем разделе более удобно нумеровать компоненты вектора f -:нcлyш от 1 до п и обозначать элементы матрицы А величинами Оц, (Ji, Oon i.

13 Блейхут Р.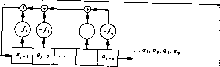

Подета.нть ..... .

Рис. 11.4. Авторегрессноиный фильтр.

При фиксированном t это уравнение является уравнением авторе грессионного фильтра, который может быть реализован в вид линейного регистра сдвига с обратной связью, в отводах которо! стоят умножители на компоненты вектора f.

С этой точки зрения задача решения данной теплицевой системй уравнений становится задачей построения показанного на рис. II4 авторегрессионного фильтра, на выходе которого формируется з. данная последовательность символов. Если теплицева матриц обратима, то существует точно один авторегрессионный фильтр удовлетворяющий данной системе уравнений. Если матрица Heoij ратима, то таких решений может существовать много или не суще! ствовать ни одного. Однако, алгоритм Берлекэмпа-Месси всегда в качестве решения дает кратчайший авторегрессионный фильтра удовлетворяющий данным уравнениям. Отводы этого фильтру описываются вектором f, содержащим не более п }1енулевых кощ понент, если исходная теплицева система имеет по меньшей мера одно решение, и большее, чем п, число ненулевых компонент /, ( > п, если исходная теплицева система не имеет решений. А

Любая процедура построения авторегрессионного фильтр! является также методом решения рассматриваемого матричногм уравнения с заданным вектором f. Мы сейчас опишем такую npoj цедуру построения регистров сдвига. В процедуре не предпол гается наличие каких бы то ни было специальных свойств последо вательности а , а1,...,щ 1. Произвольный линейный регисти сдвига с обратной связью можно задать многочленом f (х) обрат ных связей,

/() = / + /п.г -+ +fiX+l, и длиной L регистра сдвига. Длина регистра сдвига может бытш больше степени многочлена / (л:), так как самые правые ячейкйЩ регистра могут не включаться в обратную связь.

Для построения регистра сд&ига надо определить две величины: длину L регистра и многочлен / (х) обратных связей степен

f W < Обозначим эту пару через (L, f [х)). Надо Hafltri

= Or - Йг = °г -Г

Эквивалентно,

Дг =

Если Д = О, то полагаем fl (х)) = (-.л, ()) и за-

вершаем этим г-ю итерацию. В противном случае изменим весовые множители в цепи обратной связи регистра сдвига по правилу.

;(г)(;() = /(-1)(х) +Лх7< -ЧМ. где А - элемент поля, ( - целое число и fi -) (х) - один из многочленов обратной связи, встречавшийся ранее в списке регистров сдвига. 13*

регистр сдвига с обратной связью, который при соответствующих начальных условиях порождает заданную последовательность йо- <2п~\ и является прн этом кратчайшим.

рассматриваемая процедура построения является рекурсивной. Для каждого г, начиная с г = 1, мы будем строить регистр сдвига, порождающий последовательность а, а. Регистр сдвига минимальной длины, порождающий последовательность Gq, .... ar, обозначим через {L {х)). Этот регистр не обязательно должен определяться однозначно; воз.можно существование нескольких таких регистров с одной и той же длиной. К началу г-го шага имеется список регистров сдвига

(L /О) (X)), (1 /(21 (X)).....(L, i, /f-i) (X)).

Алгоритм Берлекэмпа-Месси вычисляет новый кратчайший регистр {/-г- Л * [х)), генерирующий последовательность о.....а,.

Д.пя этого используется самый последний из вычисленных регист-ftoG, в котором по мере надобности модифицируются длина и весовые множители в отводах.

На г-м шаге вычисляется следующий элемент на выходе (г - 1)-го регистра сдвига:

Я = -б/Г .-/.

Так как может быть больше степени многочлена (х), то некоторые члены суммы могут быть равными нулю. Эту сумму следовало бы записать с пределами суммирования от 1 до deg/(г-1) (х). Мы, однако, выбрали менее громоздкое обозначение.

Пусть Д, обозначает разность между требуемым элементом на выходе Or и истинным элементом, полученным ка выходе самого последнего регистра сдвига: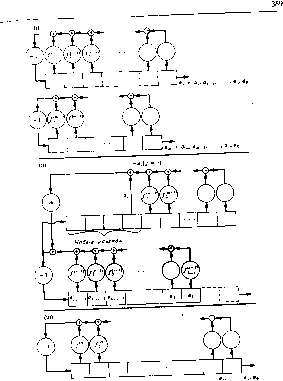

iHc. 11.5. Конпрукция Берлекэмпа-Месси.

ций m заменяется на г. хропрмой 113 2, которая

Точное описание процедуры дается т<:°Р ° . регистру утверждает, что эта процедура приводит к наименьшему реги i-j

Используя этот новый многочлен, определим

Теперь все готово для определения величин I А. Выб рем т меньше г и такое, что Д Ф 0; выберем также / = г - i и Л = -Д Д Тогда

Д; = Дг - 4 Дт = О,

так что новый регистр сдвига будет генерировать последователи ность а Qr а,. У нас остался произвол в выборе т, дл1 которого Д 0. Выбрав в качестве т номер ближайшей итера ции, для которой выполнялось условие L > получим

каждой итерации регистр сдвига минимальной длины, однако т кое усовершенствование требует дополнительных рассуждени и будет описано позже.

Практическая интерпретация того, что было изложено до на стоящего момента, представлена на рис. 11,5. Два регистрасдвигаЗ отвечающие итерациям с номерами т и г, показаны на фрагменте(1 рисунка. В качестве т-й итерации выбирается та, при которой ре гистр сдвига /l -! (х)) не способен генерировать комп

ненту о , и минимальная длина регистра сдвига, генерирующет требуемую компоненту при т-й итерации, больше L. Будем также считать, что регистр сдвига (L, i, f- (х)) не способен ге1 нерировать компоненту а так как в противном случае мы не ДОд жныничего с ним делать.

На фрагменте (ii) рис. 11.5 регистр сдвига (/. /< -) {хЩ превращен во вспомогательный регистр путем увеличения его дли- ны, позиционирования и такого изменения его выхода, которо позволяет скомпенсировать неспособность регистра (L, /<-) (х) генерировать компоненту а. Отметим, что вспомогательный ре;:] гистр имеет дополнительный отвод с весовым множителем еди- ница, соответствующим коэффициенту /о ~ . На протяжении пер ; вых г - 1 итераций в остальных отводах цепи обратной связи формируется отрицательное значение соответствующей этому до полнительному отводу величины, и поэтому на выходе вспомогЭ -тельного регистра формируется последовательность нулей. При; г-й итерации эти ве.1ичины взаимно не уничтожаются, и выход; вспомогательного регистра оказывается ненулевым. Коэффициент! А выбирается таким образом, чтобы его добавление к г-му выход-f ному сигналу обратной связи главного регистра сдвига приво--дило бы к получению нужной компоненты а,.

На фрагменте (iii) рис. 11.5 показано, как два регистра сдвига, изображенные на фрагменте (ii), сливаются в один регистр, что в силу принципа суперпозиции не меняет общего поведения схемы.-