Матрицу и оба вектора можно опять разбить на блоки, чтобы выявить лежащую в основе алгоритма повторяющуюся блочную структуру. Специальные свойства стоящего справа вектор-столбца, формируемого из элементов теплицевой матрицы, позволяют вдвое уменьшить необходимые в алгоритме Левинсона вычисления, так как в итерации включается только один многочлен. В рассматриваемом виде теплицевы матрицы часто встречаются в задачах спектрального анализа, и в этих случаях полезен алгоритм Дурбина.

r-ii шаг алгоритма Дурбина начинается с решения следующей усеченной задачи:

Оо 01 Ol

в] Оо а,

Следующая итерация начинается с уравнения

определяющего переменную у,. Целью итерации является такая модификация вектора f<0, при которой величина у, становится равной 0,.1. Пусть 1 +) задается равенством

..... j - up<iiD / г И fj, 1ак, чтооы регенерировать желаемый вид уравнений, то мы построим хороший алгоритм Но при некоторых у, и у; имеет место равенство

Рис. 11.2. Алгоритм Дурбина.

е алгоритм Лурбит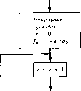

Для обеспечения нужного равенства fc, и в окончательном виде надо выбрать так, чтобы выполнялись условия

- Рг = О и

Y. = - i; fa v; = - S l: !-

Стедовательно, ft и надо полагать равными

Выписанные равенства позволяют продолжить решение г-го шага до решения (г + 1)-го шага, так что тривиальное решение нулевого шага рекурсивно продолжается до решения п-го шага. Это завершает построение алгоритма Дурбина. Окончательная представлена блок-схемой на рис. 11.2.

11.2. Алгоритм Тренча

В зависимости от наличия различных дополнительных свойств теплицеву систему уравнений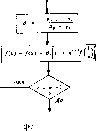

Стоп

рма алгоритма

можно решать многими различными алгоритмами. В разд. 11.1 был рассмотрен случай, когда теплицева матрица симметрична. В этом случае применим алгоритм Левинсона или Дурбина. В настоящем параграфе рассматривается более общий случай, когда

А =

Лкалогично можно разбить на блоки обратную матрицу В* = в< = ------1-----

Нашей целью является описание блоков этого последнего разбиения.

Теорема И.2.2. Блоки обратной матрицы В удовлетворяют равенству

Доказательство. Так как АВ) = I, то имеет место равенство

Следовательно,

Матрицу Mi можно исключить, выразив ее через обратную к дк-!) матрицу В *. Умножая первое уравнение на В- слева, получаем

Теперь утверждение теоремы следует непосредственно из второго из выписанных уравнений. □

До сих пор мы мало что предполагали о матрице В* , требовалось только существование матрицы В* -. Теперь для построения рекурсивной процедуры вычисления матрицы В(> по ее полугранице воспользуемся свойством персимметричности.

Теорема П.2,3. Пусть В обозначает матрицу, обратную к теплицевой матрице. Тогда В полностью определяется своей верхней полуграницей по восходящей рекурсии

1 У ~ I = 1, ..., rt - 1,

Ь1+\.ш = Ьг/ 4--[b+b b+b ], . ;j 1,

теплицева матрица не является симметричной. В этом более общем случае алгоритмом решения является алгоритм Тренча. В своей наиболее полной форме алгоритм Тренча вычисляет обратную матрицу А и вектор f. Мы остановимся только на вычислении матрицы А .

В общем случае не всякая теплицева матрица симметрична, но всякая теплицева матрица персимметрична. Матрица называется пгрсимметричиой, если стоящие cимзeтpичнo относительнд побочной диагонали ее элементы равны. Если (п X п)-матрит А персимметрична, то ац -- ani- n-i-i~i- Другими словами, матрица А персимметрична тогда и только тогда, когда JAJ - А, где J - обменная матрица той же размерности, что и А. Матрица, обратная к теплицевой, в общем случае теплицевой не является, но остается персимметричноп.

Теорема 11.2.1. Обратная к персиммгтричной матрице А является персимметричной.

Доказательство. Пусть J обозначает обменную матрицу той же самой размерности, что и матрица А. Напомним, что = I, так что =- J. Но JAJ = А. Счедовательно, JAJ = А и матрица А - является персимметричной. □

Другое свойство, которое сохраняется при обращении теплицевой матрицы, состоит в том, что она полностью определяется своей границей. Более точно, она полностью определяется заданием своих первой строки и первого столбца или своих последней строки и последнего столбца. В продолжение этого раздела дается доказательство этого свойства и затем выписывается рекурсивная процедура вычисления матрицы по ее нижней полугранице, состоящей из последней строки и последнего столбца. Для вычисления матрицы А в алгоритме Тренча используется полуграница матрицы А.

Определим вектор-столбцы и а длины г - 1 каждый равенствами

а = (fli, a-i, аэ.....а.хУ,

а = (а 1, дз, a(r-i)) . Пусть и а обозначают два вектора, компонентами которых являются компоненты векторов а+ и а соответственно, выписан- , ные в обратном порядке. Иными словами, а+ = Ja и а = Ja , где J равно обменной матрице размерности (г- 1) X (г- 1). Матрицу А! можно следующим образом разбить на блоки:

и своей нижней полуграницей по нисходящей рекурсии

= b,; + -i-[b+bl-b+bl], j];

где первая и последняя строки матрицы ровны соответственно Фа, bj и (Ь , i-g), а первый и последний столбцы матрицы равны соответственно (бд, Ь) и (Ь+, Ь).

Доказательство. В теореме 11.2.2 мы уже доказали, что

I j -+-.- -.

зсГьвГ -Р --рич ой,.о можно также

Второй дает

/ = 1..... - 1.

Исключая элементы Ь/~\ приходим к равенствам

о ; = 1, л- 1,

которые теперь содержат только помеченные индексом г величины. Эти равенства задают восходящую рекурсию. Аналогично строится нисходящая рекурсия, и это заканчивает доказательство. □

Доказательство содержит еще один информативный фрагмент, который будет ниже испо.чьзован. Выражая стоящий в первой строке и первом столбце элемент из первого равенства, получаем уравнение

Так как hbL = ЬьГ и согласно второму равенству &п * = Ьо\ то оно может быть переписано в виде

связывающем величины 6о и Ьа .

Теперь нам нужно построить алгоритм, вычисляющий полу-границу матрицы В по полугранице матрицы А ). Но у нас уже выписаны уравнения, связывающие границу матрицы В<) с границей матрицы А ), так что для построения этого алгоритма нам остается только исключить матрицы A( l и М. Такое исключение можно выполнить, вводя обратно полуграницу предыдущего шага итераций.

Теорема П.2.4. Полуграница матрицы следуюшим рекуррентным уравнениям:

В* удовлетворяет

(iii) bV bt + Л7(ь;1> ) .

Доказательство. Третье уравнение уже. было выведено как следствие из теоремы 11.2.3. Из соображений симметрии ясно, что если выполняется первое равенство, то выполняется и второе. Его можно получить тем же самым способом. Следовательно, надо доказать только первое равенство. Начнем со второго в множестве полученных в доказательстве теоремы 11.2.2 четырех равенств:

-1X4= й.

Так как .матрица А -> является персимметричной, то это равенство можно также переписать в виде

A - X + aW = 0,

откуда

Теперь воспользуемся снова уже применявшимся ранее разбиением матрицы В** -

где а+ записан в виде вектора а! * с одной дополнительной компонентой. Это уравнение уже определяет искомую рекурсию,