Стандартный метод решения системы п линейных уравнений с п неизвестными состоит в записи этой системы в матричном виде, Af = g, и отыскании решения либо с помощью обращения матрицы, \ = Ag, либо с помощью метода Гаусса. Сложность стандартных методов обращения матрицы пропорциональна . Иногда матрица имеет такой частный вид, что им можно воспользоваться для построения более быстрого алгоритма.

Система линейных уравнений называется теплицевой, если ее матрица А теплицева. Задача решения теплицевой системы урав. нений возникает во многих приложениях, включающих спектраль- ное оценивание, линейное предсказание, построение авторегрессионных фильтров и теорию кодов, контролирующих ошибки. Так как теплицевы системы уравнений имеют очень частный вид, то для их решения существуют методы, которые намного лучше общих методов решения систем линейных уравнений, Эти методы, составляющие предмет исследования в данной главе, справедливы для произвольного поля, \

Рассматриваемые в настоящей главе алгоритмы несколько отличаются от тех алгоритмов, которые мы построили для вычисления свертки или преобразования Фурье, Свертка к преобразование по существу сводятся к матричному умножению, а в данной главе рассматривается задача решения системы линейных уравнений.. Поэтому неудивительно, что мы не сможем прямо воспользоваться построенными ранее алгоритмами, хотя такой метод, как дублирование, окажется полезным.

11.1. Алгоритмы Левинсона и Дурбина

TPnlt РЩ вертки или спектрального оценивания со-

Smo Р системы уравнений, зад

ваемои матричным равенством

Af = <?,

L -..,

Вычислительная задача состоит в вычислении вектора S по заданным вектору g и теплицевой матрице А. Одним из возможных методов решения, конечно, является обращение матрицы А, однако, практически п может быть больше 100 или даже 1000, так что важно отыскать более эффективные методы решения задачи.

Аморитм Левинсона является эффективным алгоритмом, применимым в том частном случае, когда матрица А является одновременно теплицевой и симметричной. В этом случае система уравнений записывается в виде

Разделение матрицы и векторов на блоки здесь сделано для того, чтобы подчеркнуть лежащую в основе алгоритма повторяемость структуры. На каждом шаге (итерации) к матрице А добавляется потовина границы , состоящая из новой строки Снизу и нового столбца справа. Используя обменную матрицу J, уравнение At - °g можно переписать -в виде JAJJf Jg, и JAJ = А, так как матрица А является симметричной и теплицевой. С.чедовательно, имеет место также равенство

Эта форма уравнения также будет использоваться прн построении алгоритма Левинсона. .Алгоритм оперирует с (г X /-)-подматрицами матрицы А вида - в, ,.. о,.,]

а, Оо а, ... д.-! i А = 10: fli ao . i

БЫСТРЫЕ МЕТОДЫ РЕШЕНИЯ ТЕПЛИЦЕВЫХ СИСТЕМ

где А представляет собой теплицеву (п X /1)-матрицу

где верхний индекс г указывает на то, что вектор является решением г-го усечения задачи. Ясно, что если даже и является решением усеченной задачи, он не равен усечению решения f исходной задачи. Алгоритм Левинсона рекурсивно модернизирует t** * таким образом, что f > равно решению исходной задачи.

Помимо вектора i * в итерациях алгоритма Левинсона участвует несколько рабочих переменных, задаваемых следуюгцим образом. Скалярные рабочие переменные обозначаются через а, и у/, рабочий вектор длины г обозначается через t. Все эти рабочие пЬременные выбираются на каждом г-м шаге так, чтобы выполнялось следующее дополнительное матричное равенство:

где в стоящем в правой части равенства векторе все за исключением одной компоненты равны нулю. Введение рабочего вектора fi и дополнительного уравнения является разумной идеей, позволяющей продолжать итеративный процесс. Мы хотим итерации организовать так, чтобы все уравнения имели одну и ту же форму. Следующая итерация начинается с уравнения

которое определяет Vr, и с уравнения

которое определяет и в правой части которого стоит вектор, все внутренние компоненты которого равны нулю. Еслн 7 = gr и Рг О, то и t + равны соответственно f и t<, но

с добавленными нулевыми компонентами, увеличивающими их длину, в этом случае итерация завершается. В противно.м случае векторы и t** должны быть модифицированы.

Как всегда в рекурсивном алгоритме, выберем начальные значения всех переменных так, чтобы при г = О выполнялись все уравнения, и предположим, что эти уравнения выполняются к концу {г - 1)-го шага итераций. Нам надо только показать, как надо модифицировать рабочие переменные, чтобы эти уравнения выполнялись и к концу г-го шага. Но мы можем также записать уравнения

Из этих уравнений можно сформировать следующую итерацию. Пусть для подлежащих дальнейшему выбору констант и ft.

цию. Пусть дл выполняется

которые получаются из матрицы А отбрасыванием последних п - г столбцов и такого же числа нижних строк.

Алгоритм Левинсона является итеративным; эти итерации индексируются буквой г. На г-м шаге алгоритм Левинсона вычисляет решение г-го усечения задачи:

376 Гл. 11. Быстрые методы решения теплицевых систем Тогда

b Хнс : бираться так, чтобы выпол-

и a.+i = а, - р,. Наконец, положим

где константа к, также подлежит вычислению; тогда

так, ; ? Р-- ,- *з должно быть выбрано

д s+i ~ Это завершает итерацию Алгоритм Левинсона подытожен а%с. П.ьнТнем векторы

Сложность r-ro прохода по ветви пропорциональна г, и всего имеется п проходов. Следовательно, сложность алгоритма Левинсона пропорциональна п. Шаг рекурсии приводит к неудаче только тогда, когда возникает деление на нуль, что происходит только тогда, когда одна из гласных подматриц вырождена.

Алгоритм Левинсона применим в любом поле. В частности, в поле комплексных чисел его можно использовать именно в том виде, в котором он был выписан. Однако в связанных с комплексным нолем приложениях симметричная теплицева матрица возникает не часто; более распространенной в этом случае является эрмитова теплицева матрица. Алгоритм Левинсона применим и в этом случае, но с переходом в соответствующих местах вычислений к комплексно сопряженным величинам. Реконструкцию алгоритма для этого случая сделать легко.

Иногда вместо алгоритма Левинсона лучше воспользоваться так называемым алгоритмом Дурбина. Это возможно в тех случаях, когда матрица симметрична и теплицева, а вектор в правой части формируется из элементов теплицевой матрицы так, что уравнение принимает следующий вид: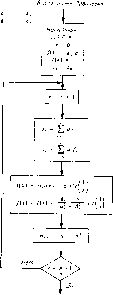

Выход

Рис. ПЛ. Алгоритм Левинсона.