. Гл. 10. Быстрые алгоритмы, основанные на стратегии дублировании

Вход

* = li deg/(*)l

/W - лг-[Л*) - (Л) mod х)) Ч) = - (j(jt) mod **)]

ПрвЦйУ1Ш

ПояоВина

\ A(Jr)

Рнс. 10.8. Процедура Половина ЕвкАлг.

шение о немедленном разбиении задачи или о выполнении стандартной итерации алгоритма Евклида, поскольку процедура разбиения и дублирования неприменима. Последнее решение принимается только в том случае, когда степень многочлена g (х) меньше половины степени многочлена / (х). В этом случае стандартная итерация алгоритма Евклида на половину снижает размерность задачи, и мы ничего не теряем, поскольку процедура дублирования неприменима.

Форма полученной при разбиении второй половины задачи совпадает с формой исходной задачи, так что для ее вычисления можно опять вызвать процедуру ЕвкАлг. Первая половина задачи имеет аналогичную, но не идентичную форму, так как вычисления следует закончить, если степени многочленов слишком малы. Половину задачи можно также разбить пополам, так что мы приходим к формулировке вычислений в рекурсивном виде. Такая рекурсивная процедура показана на рис. 10.8. Обоснование этой процедуры можно провести методом индукции. Нам надо показать, что вычисляются те же самые итерации алгоритма Евклида, которые описываются теоремой 10.7.3. Это всегда выполняется при п равном 1 и 2, так как в этом случае мы движемся по левой ветви на рис, 10.8. Прп движении по правой ветви в результате первого обращения к процедуре Половина Евк.Алг согласно предположению индукции степень deg / (х) уменьшается до (п -- ft)/2, что составляет примерно 3,4 исходной степени многочлена / (х). Второе обращение к процедуре Половина ЕвкАлг завершает описываемые теоремой 10.7.3 итерации.

10.8. Вычисление тригонометрических функций

Для вычисления тригонометрических функций обычно используется некоторое разложение в степенной ряд. Такие методы сильно отличаются от рассматриваемых нами методов. Имеется, однако, ряд приложений с привкусом стратегии дублирования, для которых более подходящими являются описываемые нами методы.

Первый из рассматриваемых нами методов дается алгоритмом одновременного вычисления значений функций sin G и cos 9 при заданном угле 6. Процесс вычисления основывается на тригонометрических тождествах для удвоения угла

sin 29 = 2 sin в cos 6, cos 26 = 1-2 sin 9,

sin 29 = 2 sin e - 2 sin 9 vers 9,

vers 29 = 2 sin 6,

где vers 9=1 - cos 6.

Для вычисления начальных значений данный угол 9 делится на некоторую степень двух и используются приближенные фор-

мулы для малых углов: sin-=-

vers-- = 0. 2

Точность алгоритма управляется выбором числа т. Величина угла 9 выражается в радианах и расположена в пределах ±п. Алгоритм автоматически помещает результат в правильный квад-

рант, так что не требуется никакого специального определения квадранта. Окончательным результатом работы алгоритма является вычисление sin 8 и I - cos В.

Для того, чтобы числовые величины не становились слишком малыми, введем новые переменные

>п =(vers8) . При этом рекуррентные уравнения принимают вид

где m обозначает полное число шагов рекурсии, и начальные условия равны Хо = Э, Fo = 0. На первой итераций точность алгоритма определяется погрешностью начального приближения и равна (Хо)в = - (1/6) (в/2 ). Эта погрешность приводит к финальным погрешностям, ограниченным сверху величиной (1/6) Л32-2 :

(sin е), < пЧ , (cos 9), < -i- л32-2 ,.

Следовательно, если при умножении обеспечено достаточное число точных битов, каждый шаг итерации увеличивает точность в двух битах.

Второй тригонометрический алгоритм представляет собой метод поворота. Его можно использовать для вычисления декартовых координат точки, повернутой на угол 8,

.у

или для вычисления полярных координат точки, заданной декартовыми координатами,

e = arctg, r = /F+7. Алгоритм состоит из некоторых вычислений и проверки логических условий- В основе алгоритма лежит тот факт, что тригонометрические тождества

Sin 9 - и cos 8 = -

11 -I- tg= 9 Kl -Ь tg 9

позволяют легко вычислить поворот вектора на конкретный угол е = arctg (2). В этом случае

sin [arctg 2-J =

V 1 1- (2-*)-

И cos (arctg 2 ] =

Vn-(2- )2

Рис. 10.9. Алгоритм поворота координат.

так что поворот вектора (х, у) на угол 9, = arctg 2- задается равенствами

Vn-(2- )

j[x + 2-i/], = [j,-2-xl.

/rT(i=

Для поворота на отрицательный угол arctg 2 используются те же уравнения, но с заменой знака у 2 . Эго не влияет на величину стоящего перед скобкой множителя. Длина вектора умножается на фиксированную константу.

Произвольный угол В может быть представлен в виде

9 = ±90°+ S (± arctg 2-)

. i sarctg2- = SA.

где = -1 О I..... I равно 1 или -1, а 9s затабулированы

на рис. Ю.Э.поворот на угол 9 просто сводится к поворотам на каждый из углов 9t с направлением, определяемым ь.

Независимо от знака каждого индивидуального поворота после m итераций усиление равно

П /1+2- . *=1

В окончательном виде алгоритм показан на piic. 10.10. Правило поворота вектора на первом шаге на угол ±90 несколько отличается от правила остальных поворотов. В дальнейшем решение

Вход

Вод Позорот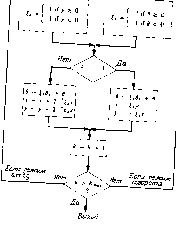

Рис. 10.10.

О повороте на угол 0 или -0l принимается в зависимости от зна- -ков координат д: и г/. Это определяет дальнейшее сложение или вычитание с умножением на скаляр. Так как скалярный множитель равен 2 *, то умножение сводится к двоичному сдвигу, так что алгоритм почти не содержит умножений. Даваемое алгоритмом представление величины усиления известно. Оно может быть нивелировано умножением на обратную величину после выполнения -всех шагов алгоритма. В больших задачах еще лучше упрятать его в константы, встречающиеся в других местах.

Для вычисления arctg {xly) вектор (д:, у) на каждой итерации вращается в том направлении, которое уменьшает текущее значение координаты у, а формирование угла 6 проводится суммированием величин 6ft с учетом их знаков.

Задачи

Найти алгоритм дублирования для умножения вектор-столбца на тепли-цеву матрицу.

Провести сортировку списка {3, 1,5.2,7, 3, 9, 8, 2, 6, 1, 4, 9, 2, 5, I}. используя алгоритм слияния.

а. Привести блок-схему БПФ-алгоритма Кули - Тьюки по основанию два с прореживанием по частоте в виде алгоритма дублирования.

б. Привести блок-схему алгоритма дублирования в рекурсивной форме для вычисления фильтр-секЧин, длина которой равна степени двух.

в. Привести блок-схему алгоритма дублирования в рекурсивной форме для вычисления произведения многочленов от двух переменных.

Пусть п равно степени двух и пусть а и й - два произвольных целых числа, запись которых содержит п позиций- Найти эффективный алгоритм умножения чисел а и 6, используя дублирование.

Разработать алгоритм транспортирования матрицы на процессоре, который может одновременно запоминать четыре столбца из таблицы. Построить блок-схему алгоритма. Сколько необходимо обменов столбцами? Сколько умножений потребуется для вычисления следующего преобразования координат?

Используя приведенный на рис. 10.10 алгоритм, вычислить arctg (2). Установить точность алгоритма, сравнивая вычисленное значение с истинным.

Используя алгоритм Штрассена, вычислить произведение матриц

10.1. 10.2, )0.3,

10.4. 10.5. 10.6.

10.7. 10.8,

Замечания

Стратегия деления задачи пополам и дублирования является одной нэ основных и появилась во многих работах. Данная короткая глава только затрагивает этот раздел общей теории алгоритмов. Более широкое введение можно найти в работах Кнута {1968) и Ахо, Хопкрофта и Ульмана (1974). Общеизвестные примеры алгоритмов дублирования и сортировки, такие как рассмотренный алгоритм слиянием, или как алгоритмы пирамидальной сортировки и быстрой сортировки, были введены Унльямсоном (1964) и Хоаром (1962) соответственно. Известны и многие другие алгоритмы сортировки. Описание БПФ-алгоритма Кули-Тьюки с точки зрения стратегии дублирования предложил Стейглиц (1974). Фндуччна (J972) применил к построению БПФ-алгоритма Кули - Тьюки полиномиальные идеи алгоритма Герцеля. позволившие использовать стратегию деления задачи пополам и дублирования. Стратегию дублирования для задачи транспонирования матрицы использовал Эклунд (1972). Первая усиленная с помощью стратегии дублирования форма алгоритма Евклида появилась в книге Ахо, Хопкрофта и Ульмана в связи с вычислением наибольшего общего знаменателя.

Алгоритм поворота вектора используется уже многие годы под названием cordic algorilhms и обычно приписывается Волверу (1959); детальная его проработка выполнена Волтером (1971). Алгоритм дублирования для вычисления синусов и косинусов взят из работы Блейхута и Волдекера (1970).