
 |
|
|
Главная -> Вычислительные алгоритмы 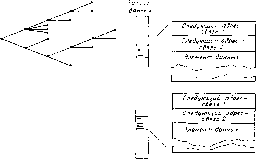 Корень Рис. 10.3. Дерево. Рис. 10.4. Двойной связанный список. Список, все элементы которого являются числами, часто называется вектором. Если все элементы списка принадлежат некоторому конечному алфавиту, список иногда называется цепочкх>й. Цепочка не обязательно имеет фиксированную длину, но длина вектора обычно фиксирована.,Различие между вектором и цепочкой лежит скорее в применении, чем в существе дела. Списком переменной длины называется список, длина которого не фиксирована, а со временем растет или уменьшается. Список переменной длины может расти или укорачиваться путем добавления новой позиции в любую точку списка или удалением позиции из любой точки списка, но во многих случаях позиции добавляются или удаляются только на двух концах списка. Список, добавление или удаление позиций в которо.м происходит только на одном конце, - скажем, в вершине - называется стеком, или обратным списком, или последним-пришел-первым-ушел-бу-фером. Список, Б котором добавление позиций происходит на одном конце, а удаление на другом, называется очередью, или первым-пришел-первым-ушел-буфером. Деревом называется такая структура данных, в которой за каждой позицией могут следовать одна или более позиций, называемых потомками; пример графического изображения такой структуры приведен на рис. 10,3, Каждому узлу соответствует позиция данных, и каждая позиция имеет в качестве своих потомков другие позиции, с которыми она связана. Возможна ситуация, в которой несколько узлов дерева соответствуют одной и той же позиции данных. В противоположность дереву каждая позиция списка может иметь только одного пото.мка. Позиция данных в списке или в дереве может быть достаточно сложной, включая, возможно, текст на естественном языке; но с точки зрения исследования структуры списков каждая позиция рассматривается как некая единица. В памяти вычислительного устройства списки и деревья запоминаются с помощью некоторых имен, присваиваемых позициям; хорошими именами являются адреса ячеек памяти, в которых начинаются данные позиций. Список (или дерево) запоминается в виде последовательности имен позиций, входящих в список. Список не обязательно запоминать в непосредственной близости к позициям данных. Другим, иногда более удобным методом, является метод непрямой адресации, называемый связанным списком; он показан на рис. 10.4. Позиции данных появляются в произвольном порядке, и каждый вход начинается с адреса следующей позиции данных списка. На рис. 10.4 показан двойной связанный список. В двойном связанном списке данные записаны двумя способами - скажем, в алфавитном и хронологическом порядке - но не обязательно запоминаются дважды. Если список часто пересматривается, то удобнее пользоваться связанным списком, так как это позволяет не двигать данные. Организация стека даже из сложных позиций данных реализуется простым присваиванием адреса первой позиции данных и привязыванием к каждой позиции данных адреса следующей по списку позиции данных. Для записи новой позиции данных в вершину стека надо просто привязать адрес предыдущей вершины к новой вершине и изменить адрес первой позиции данных на адрес новой позиции. Для извлечения позиции данных нз вершины стека надо обратить процедуру. 10.3. Быстрые алгоритмы сортировки Задача сортировки формулируется следующим образом. Задана произвольная последовательность из п элементов, выбранных из множества, на котором имеется некоторый естественный порядок. Необходимо переупорядочить заданную последовательность в том же естественном порядке. Алгоритм сортировки может относиться непосредственно к позициям данных и перезаписи их в памяти, а может и не затрагивать позиции данных, а оперировать только с некоторыми привязанными к ним параметрами. Данные сортируются переупорядочиванием списка непрямых адресов. Сортировка переупорядочиванием адресов полезна в тех случаях, когда объем данных в каждой позиции сам по себе очень велик. Предположим, что с каждой позицией данных связан некоторый целочисленный параметр, и необходимо упорядочить позиции данных так, чтобы целочисленный параметр менялся от своего наибольшего значения к наименьшему. Любая задача сортировки может быть сформулирована в таком виде. Наивная процедура сортировки состоит в просмотре одной позиции за другой п выборе той, которой соответствует наибольшее значение параметра. Затем так же просматриваются оставшиеся позиции и находится та из них, которой соответствует наибольшее значение параметра. Это продолжается до тех пор, пока не будут рассортированы все позиции. В повседневной жизни, когда п мало, это вполне удовлетворительная процедура. Однако, среднее число шагов в ней пропорционально п. Для сортировки больших списков можно действовать намного лучше. Хорошие алгоритмы сортировки основываются на делении списка пополам и дублировании. Одним из них является алгоритм сортировки слиянием; его сложность пропорциональна величине я logj п. Разобьем список из я позиций данных на две половины и упорядочим каждую из них. Из этих упорядоченных списков половин организуем общий упорядоченный список, сливая их вместе по следующему правилу. Сравним верхние элементы в обоих списках. Выберем из них тот, который соответствует большему значению параметра, и разместим его в качестве следующей позиции объединенного списка, выбросив из той половины, где он находн.тся раньше. Так как каждая позиция попадает в объединенный список после операции сравнения, то в общей сложности придется сделать п сравнений. Следовательно, сложность С~{п) алгоритма сортировки слиянием описывается рекурсией С(я)<2С(--) + п. Э1-а рекурсия дает оценку сложности для алгоритма сортировки слиянием: С (я)< п logs п. Так как имеется только одно значение аргумента, при котором здесь выполняется равенство, то при слиянии некоторые сравнения не нужны, так что алгоритм можно немного улучшить. Тем не. менее, мы полагаем, что эта оценка является достаточно точной. Имеются другие способы разбиения задачи сортировки. В алгоритме быстрой сортировки случайно выбирается один из параметров данных в качестве основы для разбиения списка. Характеристики такого алгоритма являются случайными величинами, достатбчно хорошими в среднем, но очень медленными в наихудших случаях. Так как в алгоритме быстрой сортировки параметр разбиения . списка выбирается непосредственно из данных, то этот параметр долженбыть случаен. В противном случае можно было бы построить тестовый список, для которого быстрый алгоритм оказался бы очень пло.чим. Например, если в качестве параметра разбиения списка всегда выбирать первый вход данных, то бы- стрый алгоритм будет сортировать список чрезвычайно медленно. Быстрый алгоритм работает следующим образом. Выберем случайно из данных некоторый элемент с параметром а. Все данные, за исключением а, разделим на два подмножества: те данные, параметр которых меньше а, и те данные, параметр которых не меньше а. Упорядочим каждое из этих подмножеств и соединим их в один список, расположив позицию а между ними. Каждое 113 двух под.множеств упорядочивается по такому же правилу. Два списка, на которые разбивается исходный список, содержат по я - 1 - i и i элементов, где i - случайная величина, равновероятно распределенная на множестве 0, ... , я- 1(. Сложность формирования этих множеств пропорциональна я. Средняя сложность сортировки исходного списка из я точек равна C{n)-=An±C{i)-LC{ - I - О, где .4 - некоторая константа. Для п > 2 это приводит к следующей рекурсивной формуле для сложности С (п) алгоритма быстрой сортировки : С(я) = Ля-fС() при начальных условиях С (0) = С (1) = 0. (Иногда предпочитают полагать С (0) и С (I) некоторыми малыми константами, но это мало что меняет и никак не влияет на асимптотику сложности.) Покажем, что при я > 2 величина С (я) меньше, чем 2Ап log п. Доказательство проведем индукцией: предположим, что для всех Г< я величина С (<) меньше, чем 2Ailn,i. Это справедливо для я = 2. Тогда С(п)< Ля-f.-2 Гак как функция i In i выпукла, то правую часть можно ограничить величиной вида C{n)<An + -ixln,xdx. Следовательно, С(я)< Ля-f[-1 - ] = 2ЛяIn.я. 10.4. Рекурсивное быстрое преобразование Фурье по основанию два Комплексное преобразование Фурье по основанию два определяется формулой Vk= S мЧ. А = 0..... где п = 2 , m - целое число и v - вектор с комплексными компонентами. В гл. 4 мы интересовались построением алгоритмов, представляющих собой малый пакет уравнений, непосредственное применение которых позволяет вычислить преобразование Фурье , радиуса два. Этот способ очень подходит для длин п, равных 8 или 16, но может оказаться неподходящим при больших п. В настоящем параграфе мы выпишем алгоритм по основанию два в рекурсивной форме. Входные данные в комплексном виде мы выбираем потому, что при п = 32 и более эта форма алгоритма применительно к комплексным данным эффективнее, чем двойное использование БПФ-алгоритма для вещественного входа. Так же, как и в гл. 4, воспользуемся методом Винограда для разбиения вычисления преобразования Фурье на отдельное вычисление компонент с четными индексами и компонент с нечетными индексами. Для обработки компонент с четными индексами ; заменим А на 2ft и запишем V = е (V, + ,+ /2)* = О..... /2 - 1. Мы получили n/2-точечное преобразование Фурье нового вектора, компоненты которого равны Vi + и<+п/2, так что для их вычисле-ния требуется п/2 комплексных сложений. Для обработки компо- нент с нечетными индексами заменим А на 2ft + 1 и запишем п/2-I П/2-I 2.1= S ,;(0 2 ,oi( +l)W>, ft = = о.....л/2-1. Эти две суммы будут рассматриваться отдельно. Для их сочетания потребуется еще п/2 комплексных сложений. В первой сумме выписанного уравнения необходимо вычислить только первые компоненты для ft = О, п/4 - 1, так как Б дальнейшем они повторяются. Эти компоненты представляют собой (п/4)-точечное преобразование Фурье вектора с компонентами для вычисления последнего вектора требуется (3/4) п - 8 вещественных умножений (так как это вычисление содержит п/4 - 4 комплексных умножений, каждое из которых может быть выполнено с тремя вещественными умножениями, и два комплексных умножения, для вычисления каждого из которых нужно только два вещественных умножения) и столько же сложений. Основная часть рассуждений связана с вычислением промежуточного результата, п/2-I Так как порядок элемента м равен п, то вычисления в показателе степени должны проводиться по модулю п, где п = 2 . Все эти вычисления представляют собой умножения нечетных чисел по модулю 2 . Согласно теореме 5.1.8, относительно операции умножения по модулю 2 множество нечетных чисел образует группу, изоморфную группе Zz X z ~ и, следовательно, имеет две образующие, В качестве таких образующих можно выбрать 3 и -1; тогда множество показателей степени образует мультипликативную группу 3 (-1): I = О, 2 - 1; / = О, 11, групповой операцией в которой является умножение по модулю 2 . На входных и выходных индексах это задает соответственно подстановки 2i + 1 = 3(-1) и 2ft + 1 =3-(-1)-. При таком представлении индексов предыдущее уравнение приводится к виду I , , г = 0.....2 -2- 1, где элементы , и И/, с двумерных таблиц равны тем компонентам и Oji+i, индексы которых определяются выписанными выше подстановками. Рассматриваемое уравнение преобразуется при этом в двумерную циклическую свертку: t-{x. y) = g{x, y)v{x, у){тойх --~ l)(mody2-l), где g (х, у) равен обобщенному многочлену Рейдера, 1 г -!-! g{x, {/) = S S 12 Блейхут Р. Средняя характеристика алгоритма быстрой сортировки асимптотически лучше средней характеристики алгоритма сортировки слиянием, но в наихудшем случае характеристика становится намного хуже.
|