Некоторые хорошие алгоритмы удается строить на основе стратегии, которая дублирует алгоритм решения половины задачи. Выберем объем задачи п в качестве параметра и разобьем, если можно, задачу на две подзадачи объема п/2 той же самой структуры, что и исходная задача. Если решения этих подзадач можно скомбинировать в решение исходной задачи, то получается алгоритм решения данной задачи, который часто оказывается эффективным. БПФ-алгоритм Кули-Тьюки по основанию два можно понимать как алгоритм, полученный разбиением задачи на две половины и дублированием, так как п-точечный алгоритм строится из двух (п/2)-точечных БПФ-алгоритмов. Алгоритм итерирования фильтр-секций также имеет эту структуру, так как п-фильтр-секция строится из двух (п/2)-фильтр-секций. В настоящей главе строятся другие быстрые алгоритмы, основанные на делении задачи пополам и дублировании. Они иллюстрируют способ построения алгоритмов, пригодных для многих видов задач.

10.1. Стратегия деления пополам и дублирования

Рассмотрим задачу нахождения многочлена р (х) степени п, заданного своими корнями р р,.....P i. Мы должны найти коэффициенты многочлена р (х) вида

p(x) = (x-p,)(*-pj...(x-p .J.

Наиболее естественным путем решения этой задачи является последовательное умножение на одночлены, начиная с какого-нибудь конца, скажем правого, согласно процедуре

р(>(х) = (х-р,)р<->(х), 1 = 1,

при начальной точке р ч (х) = (х - р ). На i-м шаге итерации такая процедура требует i умножений и i сложений, что в общей сложности приводит к (1/2) п (п - 1) умножениям и такому же числу сложений.

и рассмотрели многокаскадные конструкции прореживающих фильтров. Обзор работ по интерполяции и прореживанию можно найти в статье Кроцдьера и Ре-бинера (1981).

За исключением числа умножений и числа сложений, мы не проводили сравнений характеристик различных БПФ-алгоритмов, так как, даже если отбросить аппаратурную реализацию и рассматривать только программную реализацию алгоритма, эти характеристики зависят от точности выбранного варианта алгоритма, уровня языка программирования, архитектуры процессора и искусства программиста. Некоторые исследования характеристик были проведены Колбой и Парисом (1977), Силверменом (1977), Моррисом (1978), Навабом и Макклелланом (1979), Паттерсоиом и Макклелланом (1978) и Пандой, Полом и Чаттерджи (1983). Было бы опрометчиво заявить, что из всех этих разнообразных работ можно сделать единое заключение.

БЫСТРЫЕ АЛГОРИТМЫ, ОСНОВАННЫЕ НА СТРАТЕГИИ ДУБЛИРОВАНИЯ

Деление задачи пополам и дублирование позволяет построить более эффективный алгоритм. Предположим, что п равно степени двух, а именно я = 2 . (Процедуру легко модифицировать для других значений п, пополняя данные фиктивными входами.) Положим теперь

р(х)= П (х-р,). Р

п/2-1

(Х)= П (Х-Р ,2+,) 1=0

р (х) = р (х) р (х).

Последнее равенство в том виде, в котором оно записано, требует {n/2Y умножений. Если р (х) и р (х) вычисляются непосредственным образом, то каждое из этих вычислений требует (1/2) (п/2) ((п/2) - 1) умножений. Полное число умножений равно

(xr+24(l)(-f-0-r ( ~).

что не лучше, чем при прямом методе вычислений.

Для извлечения из стратегии дублирования какой-то выгоды надо применить лучшие способы сочетания двух частей вычисления р (х) = р (х) р (х). Но эта задача представляет собой линейную свертку, которую мы столь интенсивно изучали и которую можно вычислить не более чем с An logj п операциями, где А - некоторая малая константа. Следовательно, полное число умножений в таком алгоритме не превосходит величины

М(п) = 4nlog,n + -f (-f - l),

которая при больших п уже лучше выписанной ранее. Эго число можно уменьшать еще дальше, применяя к вычислению каждого из многочленов р (х) и р (х) ту же самую идею. Каждая из этих задач может быть разбита на две и вычислена по алгоритму, сочетающему содержащие А (п/2) log, (п/2) операций решения двух половин, что дает в итоге меньше чем An logj (n/2) операций. Продолжая таким образом, мы уменьшим число умножений до

М (п) = Л 2 log2 (1/20 = -4 (log! - logs )-

При не очень малых п эта величина меньше, чем (1/2) п (п - 1), так что стратегия разбиения задачи пополам и дублирования позволила построить улучшенный алгоритм.

На рис. 10.1 приведена схема организации вычисления произведения многочленов с помощью рассмотренной процедуры дублирования. Эта схема является хорошим примером так называемых рекурсивных процедур. Рекурсивная процедура представ-

Bbtjoe процедуры По/гиКозср

ВензоЗ процедуры ПслиНоуф

Вызов процедуры ПолоКозф

Вызов свертка

pfx)~pU)pUx)

т - г \

Во- туа-tXiiSaHtje данные из стена

Выход

Рис. 10.1. Процедура ПолнКоэф,

Замечания: Г - глобальная переменка г+га-I

Процедура ПолнКоэф вычисляет П U - 0 ,)

Выэое

для п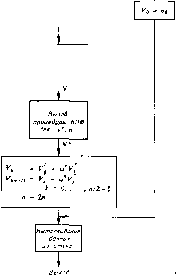

Рис. 10,2. Процедура БПФ.

ляет собой искусный программный модуль, который не содержит точного описания каждого уровня вычислений, а описывает только один уровень, содержащий копию той же самой процедуры. Процедура обращается с вызовом к самой себе. Это предполагает запись текущих данных в виде стека, который будет описан в следующем разделе. При каждом вызове процедуры происходит проталкивание вниз существующего стека данных с целью освобождения чистого рабочего пространства.

Подобная стратегия дублирования может использоваться для решения многих задач. Если задача некоторого вычисления зависит от некоторого целого числа п, то при я = 2 можно попытаться получить ответ из ответов для двух подзадач с /г = 2 -. Рекурсивная форма БПФ-алгоритма Кули-Тьюки с дублированием выписана на рис. 10.2. Полезно проследить, насколько отличаются последовательности операций на рис. 9.8 и 10.2. Рекурсивный алгорит-м приводит к расточительному использованию текущей памяти, так как создает временный стек для запоминания результатов вычисления преобразований Фурье разных объ- емов. С другой стороны, рекурсивную форму алгоритма удобно использовать в единой программе, позволяющей вычислять произвольное преобразование Фурье по основанию два. Рекурсивная форма может быть также удобна для организации БПФ-алгоритмов по смешанному основанию, так как легко разветвляется в другие подпрограммы.

Стратегию дублирования обычно удается распространить на задачи, в которых параметр п не равен степени двух. Один из способов состоит в добавлении достаточного для превращения числа п в ближайшую степень двух числа фальшивых итераций, хотя иногда, как, например, в случае преобразования Фурье, этот способ не проходит. Можно также разбивать задачу на подзадачи другого объема, равного, скажем, трети или пятой части объема исходной задачи, но, если задача допускает, разбиение на половинки, как правило, дает лучший результат.

10.2. Структуры данных

Входящий в некоторое вычисление набор данных перед началом обработки должен быть соответствующим образом упорядочен. Данные промежуточных вычислений также подлежат определенному запоминанию; в рассмотренных в предыдущем параграфе алгоритмах дублирования для этого использовался обратный стек. Двумя основными методами организации данных являются списки и деревья. Списком длины L называется упорядоченное множество из L позиций; каждая позиция сама может представлять собой сложный набор данных, даже, в частности, тоже содержать списки.