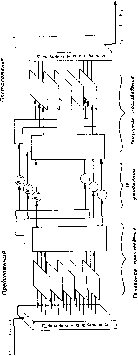= С,В,А, и Wi = С,В,А где В, и В, представляют собой диагОг ] нальные матрицы соответственно размерностей 9 и И. Тогда] большой БПФ-алгоритм Винограда записывается в виде

VI = (С, X с,) (В, X в.) (А, X А,) = (С, X С.) Вез (А, X А.).

Каждый из крайних множителей мы будем использовать в виде i кронекеровского произведения, не производя вычисления новой \ матрицы, равной этому кронекеровскому произведению. Член В, X Bs заменим, однако, на диагональную матрицу Вез.

Реализация рассматриваемого БПФ-алгоритма начинается с пе- резаписи данных в виде двумерной (7Х9)-таблицы. Первое умно-J жение каждого из 7 столбцов таблицы на матрицу Aj удлиняет i столбцы до 11. Следующее за этим умножение каждой из 11 строк на матрицу А, приводит к их удлинению до 9. Теперь данные записаны в виде двумерной (9х 11)-таблицы. Умножим поэлементно эту матрицу на 99 констант матрицы В,з, которые заранее должны быть записаны в постоянном запоминающем устройстве. (Более . точно, Вез представляет собой диагональную матрицу размерности 99, но для простоты ее здесь лучше рассматривать как (9 X 11)-таблицу, элементами которой служат упорядоченные соот- ветствующим образом элементы диагонали матрицы Вю.)

Полученную таблицу данных уменьшим теперь в объеме, умножая сначала каждый из 9 столбцов на Сд, а затем каждую из 9 строк на матрицу С,. Это приведет к вычислению всех 63 компонент преобразования Фурье входного вектора, записанных в виде (7х9)-таблицы. Остается только переупорядочить компоненты, одновременно записывая их в виде одномерного массива.

На рис. 9.12 иллюстрируется структура использования малых преобразований Фурье в 15-точечном БПФ-алгоритме Винограда. Из рисунка ясно, как простые логические цепи многократно используются для реализации указанных функций. Аналогичную структуру можно использовать и для других длин преобразований. В тех приложениях, в которых необходимо вычислять ге-то-чечное преобразование Фурье непрерывного потока данных, можно воспользоваться конвейерной схемой. Показанная на рис. 9.13 конвейерная архитектура относится к высокоэффективному 1008-точечному БПФ-алгоритму. Такая структура может быть предложена для гипотетической радиолокационной задачи, в которой необходимо вычислять 1008-точечное преобразование Фурье бесконечной последовательности данных. Этот способ позво.гяет достигать скоростей вычисления порядка миллионов отсчетов в секунду. Входные данные распределяются по банкам 16-точечных модулей БПФ, пройдя через которые они поступают в банк 63-точечных модулей БПФ. Во время обработки данных в 63-точечных модулях в 16-точечных модулях начинается обработка следующего пакета данных. Этим достигается одновре-

Шина данных

шина данныл

Донные ft? бреметой -области

дйиишх

Буферная память

Модуль йоге БПФ

бусрврная памотй

Модуль ibточечного БПФ

буферная память

па ft ять

Модуль 63-тоие-иого 5ПФ

Буферная помять

Модуль 63-тоиеи-ного 5ПФ

буферная память

Модуль t6-точечного бПФ

Модум 63- иого 5ПФ

Данные - б частотной области

Рис. 9.13. Архитектура 1008-точечного БПФ,

менность вычисления обоих БПФ. В такую конвейерную архитектуру можно добавить параллельно работающие преобразователи, реализующие необходимые перестановки компонент данных. Тогда конвейер будет содержать четыре каскада - два для вычислений и два для перестановок компонент.

Может оказаться удобным, например, выбрать для первого банка девять 16-точечных модулей, а для второго - восемнадцать 63-точечных модулей. Тогда каждый 16-точечный модуль должен в пределах одного пакета выполнять 7 вычислений, Выбор соответствующих семи векторов с шины данных регулируется простыми методами управления памятью и циклическими выборками из памяти. Аналогично, передача данных с выхода 16-точечных модулей на центральную шину данных управляется некоторым фиксированным протоколом. Определенный протокол управляет также обработкой данных в 63-точечных модулях.

9.8. Преобразование Фурье ограниченного диапазона

Предположим, что при п временных компонентах преобразования Фурье интерес представляют меньше чем п частотных компонент. Скажем, имеется приложение, в котором обработке подлежат 10 ООО временных компонент. Это позволяет вычислить 10 ООО компонент спектра, из которых нужны не все, а, возможно, только 100. Воспользовавшись 10 000-точечным БПФ, можно вычислить все спектральные компоненты, а затем ненужные отбросить. Но лучше воспользоваться прореживающей фильтрацией и преобразованием Фурье ограниченного диапазона.

Преобразование Фурье ограниченного диапазона относится скорее всего к другой области цифровой обработки сигналов; оно не представляет собой быстрого алгоритма в том смысле, который вкладывается в это понятие в данной книге. Мы только хотим упомянуть его как некоторый другой метод, характер которого сильно отличается от изучаемых нами алгоритмов. В своем большинстве наши алгоритмы носят характер математических тождеств. Вопросы точности относятся к реализации алгоритмов, но не к их построению. Еслн ответ неточен, то это не вина алгоритма, как такового, а скорее связано с невозможностью записи чисел бесконечной длины при выполнении сложения и умножения.

В преобразовании Фурье ограниченного диапазона появляется новый феномен. Оно представляет собой не математическое тождество, а всего лишь приближенное вычисление, хотя и дает сколь угодно точное приближение. Общий вид преобразования Фурье ограниченного диапазона представлен на рис. 9.14.

Входной поток данных

Выходной спектр

Рис. 9.14. Вычисление преобразования Фурье ограниченного диапазона.

Центральной теоремой в исследованиях прореживающих фильтров является теорема отсчетов. Скорость отсчетов временного дискретного сигнала не может быть меньше скорости Найквиста. Если скорость отсчетов сделать меньше, чем удвоенная максимальная частота ненулевой компоненты, то эти компоненты начинают накладываться на компоненты с меньшими частотами, создавая фальшивый образ .

При вычислении преобразования Фурье ограниченного диапазона данные сначала пропускаются через низкочастотный прореживающий фильтр, который подавляет ненужные спектральные компоненты и сохраняет те спектральные компоненты, которые представляют интерес. Практически используемые низкочастотные фильтры, построенные методами дискретной техники, не являются совершенными низкочастотными фильтрами. Они немного изменяют нужные спектральные компоненты и не полностью подавляют нежелательные спектральные компоненты, так что преобразование Фурье ограниченного диапазона не является точным.

После выполнения прореживающей фильтрации для вычисления нужных спектральных компонент можно воспользоваться БПФ-алгоритмом малой длины. Если полоса нужных спектральных компонент начинается не с нуля, то надо просто ввести показанный на рис. 9.14 модулирующий множитель ю Это обеспечивает такой частотный сдвиг представляющих интерес частотных компонент, что они начинаются с нуля.

Задачи

9.1. Доказать, что если п равно степени двух, то п-фильтр-секция, построенная

итерацией 2-фильтр-секции, содержит М. = п сложений, описываемое рекурсией

Л (л) = 2л + ЗЛ (л/2)

умножений и число

с начальным условием Л (1) = 0.

9.2. Отталкиваясь от описанного в гл. 3 алгоритма двумерной 3-точечной линейной свертки, построить методом итерации двумерную 9-точечную линейную свертку.

9.3. Для линейной свертки можно предложить метод перекрытия, который по своему духу будет чем-то средним между методом перекрытия с накопле-

нием и методом перекрытия с суммированием. Выписать уравнения для этого гибридного метода. Каковы его преимущества и каковы недостатки?

9.4. Доказать, что алгоритм, вычисляющий три последовательных отсчета на выходе симметрического фильтра с четырьмя отводами, должен содержать по меньшей мере пять умножений.

9.5. Допустим, что имеется устройство (в виде жесткого модуля или подпрограммы) для вычисления 315-точечной циклической свертки, и что необходимо пропустить вектор, содержащий 1000 отсчетов данных, через КИО-фильтр с 100 отводами. Описать, как нужно разбить данные и организовать вход и выход устройства свертки для того, чтобы произвести необходимые вычисления.

9.6. а. Построить содержащий семь умножений алгоритм 4-точечной симметричной фильтрации вектора с четырьмя компонентами.

б. Построить содержащий шесть умножений алгоритм 4-точечной косо-симметрической фильтрации вектора с четырьмя компонентами.

5.7. Если последовательность данных d является комплексной, то автокорреляцию обычно определяют равенствами

= 0.....N -\- L~2.

Показать, как надо изменить блок-схему на рис. 9.6 для того, чтобы она стала пригодной для обработки комплексных данных.

, Для вычисления сверток можно использовать метод перекрытия с накоплением и короткие БПФ-алгоритмы, добавляя к ним некоторые поправочные члены. Используя 48-точечный БПФ-алгоритм Винограда, применить этот метод для вычисления 25 точек на выходе КИО-фнльтра с 25 отводами. Сколько сложений и умножений потребуется в таком алгоритме?

. Выписать алгоритм 3-фильтр-секции для поля комплексных чисел. Сколько вещественных сложений и умножений содержит алгоритм?

Замечания

Методы перекрытия для вычисления данных линейных сверток разбиением их на отрезки представляются естественными и использовались, по-видимому, независимо во многих работах. Стокхэм первым (1966) отметил, что сочетание БПФ-алгоритма Кули - Тьюки с теоремой о свертке дает хороший способ вы-числейия циклических сверток. Агарвал и Баррас (1974) показали, как можно одномерную свертку преобразовать в многомерную свертку, используя схему переиндексации, которую мы назвали гнездовым или итеративным методом. Эта конструкция представляет собой одну из форм секционирования по методу перекрытия с накоплением, в котором секции упорядочены в виде матрицы. Та же самая идея, но основанная на методе перекрытия с суммированием, была предложена Дюбуа и Венецианопулосом (1978) для вычисления больших циклических сверток. Конструкции хороших алгоритмов коротких секций фильтров, включая симметрические н кососимметрические фильтры, были описаны Виноградом (1979, 1980). Конструкции для интерполирующих секций фильтров являются непосредственным приложением методов Винограда к этим частным задачам. Трансформационный принцип описан Хопкрофтом и Мюзинским (]973). .Метод секционирования для вычисления автокорреляции принадлежит Рейдеру (1970). Имеется очень много публикаций, посвященных вопросам организации памяти для построения БПФ-алгоритмов. Одной из недавних работ является работа Барраса и Эшенбечера (1979).

Использование прореживания для вычисления преобразования Фурье было предложено Лю и Минцером [1978]. Они пошли дальше нашего краткого обзора