330 Гл. 9. Архитектура фильтров и преобразований ±

1° .....

Di - £ *<! *-0.....

1.-5. + л*- [йГ + (-1)о ,

* о.....п-1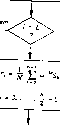

Рис. 9.6. Вычисление автокорреляций.

В таком блочном виде матричное уравнение принимает форму

tl, . . . du,

где к g (х) и к d (х) добавлены 20 нулевы.х компонент так, чтобы новое значение г = 10 020 делилось на 30. Каждый из малых блоков, например, первый

можно вычислить, используя бО-точечный БПФ-алгоритм Винограда и взяв в качестве ответа первые 30 выходных точек. Теперь рассмотрим блочную структуру

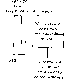Рис. 9.7. Коррелятор.

где опять дописаны нулевые блоки так, чтобы получалось число блоков, кратное четырем. Теперь надо построить алгоритм вы-i числения вида

Это вычисление идентифицируется как 4-фильтр-секция. То, что элементами, над которыми выполняются вычисления, являются матрицы, роли не играет; можно воспользоваться построенным! в разд. 9.2 алгоритмом, содержащим девять умножений и 21 сложение. Каждое из умножений является на самом деле 30-фильтр- секцией, которую мы уже решили вычислять через 60-точечный БПФ-алгоритм Винограда. Это вычисление должно быть повторено 84 раза, после чего для вычисления нужного ответа нада просуммировать все полученные ответы.

Окончательная форма этого алгоритма вычисления корреляции показана на рис. 9.7. Символами Dj и Gj на рисунке обозна-

чены преобразования Фурье блоков отрезков данных dj- и, gy. Те преобразования, которые используются более одного раза, сохраняются, а не перевычисляются. Большинство сложений выполняются в частотной области, хотя мы описывали их во временной области. Это позволяет уменьшить число необходимых обратных преобразований Фурье. .Можно еще несколько уменьшить число требуемых сложений, если умножение на матрицу постсложений в каждом из алгоритмов секций отложить до того момента, пока не будут просуммированы выходы всех фильтр-секций. Тогда эти сложения будут выполняться только один раз.

Теперь обсудим сложность такой реализации рассматриваемого вычисления, имея в виду число умножений. В общей сложности алгоритм содержит 676 обращений к 60-точечному БПФ-алгоритму Винограда, что приводит к 48 672 умножениям. Алгоритм содержит также 84-кратное использование алгоритма для 4-фильтр-секции, каждое из которых содержит девять векторных умножений, представляющих собой покомпонентное произведение 60-точечных комплексных векторов, для вычисления каждого из которых, в свою очередь, необходимо три вещественных умножения. Это приводит к 146 080 умножениям. Таким образом, полное число умножений в рассматриваемом алгоритме вычисления 120 точек корреляции последовательностей из 10 ООО отсчетов равно 194752. Для задач, в которых требуется вычисление высокоскоростной корреляции, - типа задач обработки радиолокационных сигналов, - приведенный на рис, 9.7 алгоритм можно реализовать в виде дискретно-логического устройства.

9.7. Устройства для вычисления БПФ

Хороший БПФ-алгоритм можно использовать успешно только тогда, когда удается реализовать заложенные в нем возможности. Конструируя аппаратурный модуль или подпрограмму, необходимо тщательно анализировать структуру алгоритма.

БПФ-алгоритмы Кули-Тьюки по основанию два и четыре обладают регулярной структурой и допускают относительно прямую реализацию. Алгоритм задается несколькими инструкциями. Поэтому, если в програм.мной реализации длина памяти, в которой записываются инструкции, является более важным параметром, чем время выполнения программы, то БПФ-алгоритму Кули-Тьюки следует отдать предпочтение перед другими, более быстрыми алгоритмами.

Те же соображения применимы и к аппаратурной реализации. Регулярность архитектуры устройства для вычисления преобразования может оказаться важнее общего числа компонент. Тогда опять следует отдать предпочтение БПФ-алгоритму Кули-

Тьюки в силу его регулярности. Регулярность БПФ-алгоритма Кули-Тьюки очевидным образом вытекает из его блок-схемы, показанной на рис. 9.8 для случая прореживания по времени. На всех шагах итерации используется простое 2-точечное преобразование Фурье. Основной вычислительный модуль состоит из 2-точечного дискретного преобразования Фурье и фазовращателя. Показанная на рис. 9.9 диаграмма этого модуля определила его название; он называется 2-точечной бабочкой. Алгоритм Кули- Тьюки по основанию два с прореживанием по частоте, показанный на рис. 9.10, также строится на основе подобной бабочки, диаграмма которой приведена на рис. 9.11.

Если 2-точечная бабочка задана, в виде ли программной реализации, в виде ли аппаратурного модуля, то БПФ-алгоритм Кули-Тьюки по основанию два с прореживанием по времени сводится просто к определенной последовательности прохождения входных данных через 2-точечную бабочку. При каждом таком прохождении вычисляется соответствующее преобразование Фурье, но индексы данных переставляются. На рис. 9.8 указана перестановка на входных данных, которая предопределяет вычисление выходных данных в естественном порядке. При желании можно входные данные подавать в естественном порядке, но тогда пересечения линий на диаграмме примут более сложный вид.

При написании программы БПФ-алгоритма Кули-Тьюки удобнее выбрать форму, в которой вычисляемые выходные данные записываются в памяти в переставленном виде. Перед использованием этих данных надо выполнить обратную перестановку. Другой возможностью является написание программы алгоритма в таком виде, когда на каждом шаге итерации вычисленные данные возвращаются в память в таком порядке, что адресация данных на следующем шаге итерации совпадает с адресацией на прошлом шаге. Имеется много способов таких перестановок; их детализация является существенной частью структуры программы или аппаратурного модуля. Конструктор должен решить, какая часть данных будет переиндексирована при запоминании, какая часть данных будет переиндексирована при вызове, и какая часть рабочей памяти может быть использована сверх того объема, который отведен для запоминания входного массива данных.

Большой БПФ-алгоритм Винограда не является столь регулярным, так что его реализация не может иметь такого аккуратного вида. Однако, если приступая к программной или аппаратурной реализации, тщательно проанализировать структуру алгоритма, то ее можно сделать достаточно упорядоченной. Проиллюстрируем некоторые возможности на примере построения 63-точечного БПФ-алгоритма Винограда из 7-точечного и 9-точечного БПФ-алгоритмов Винограда. Предположим, что в малых БПФ-алгоритмах Винограда матрицы профакторизованы в виде W,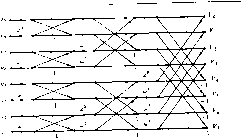

Рис. 9.8. БПФ-алгоритм Кули-Тьюки по основанию два с прореживанием по аремени.

Рис. 9.9. Двуточечная бабочка.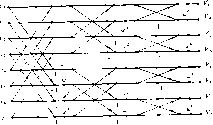

Рис. 9,10. БПФ-алгоритм Кули-Тьюки по основанию два с прореживанием по частоте.

Рис. 9.11. Двуточечная бабочка.