
 |
|
|
Главная -> Вычислительные алгоритмы виборки алгори! Малый БПФ- Малый БПФ- Час) 9 точек 1в mi 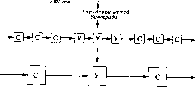 Рис. 8.9. Структура большого i008-точечного БПФ-алгоритма Винограда. Временные Малый еПФ Малый Ш>- Малый ВПФ- Чп. [с] [у] [с] - (с][у](с] Винограда Рис. 8.10. Структура другого 1008-точечного преобразования. преобразования. Этот БПФ-алгоритм содержит 3564 вещественных умножении, которое получено как произведение чисел необходимых умножений в 7-, 8- и 16-точечных БПФ-алгоритмах Винограда, удвоенное для комплексного входа. Более регулярный БПФ-алгоритм с разбиением данных на меньшие блоки приведен на рис. 8.10, В этом алгоритме сочетаются только 7-точечное и 9-точечное преобразования. 1008-точечное преобразование вычисляется затем как двумерное (63x16)-преобразование Фурье. Каждая составляющая вычисляется БПФ-алгоритмом Винограда. Полное число вещественных умножении равно 4396 = 2 (16M (63) + бЗМ (16)) 8.4. Алгоритм Джонсона-Барраса быстрого преобразования Фурье Мы рассмотрели два способа сочетания малых БПФ-алгоритмов Винограда, а именно, гнездовую схему Гуда-Томаса для взаимно простых делителей и гнездовой метод Винограда. БПФ-алгоритмы Джонсона-Барраса представляют собой целое семейство гнездовых алгоритмов, включающее в себя методы Гуда- Томаса и Винограда в качестве двух экстремальных случаев. Идея БПФ-алгоритма Джонсона-Барраса состоит в модернизации использования кронекеровского произведения для переупорядочивания последовательности вычислений. Это позволяет уменьшить число необходимых умножений, сохраняя малым число необходимых сложений. Кроме того, архитектура алгоритма позволяет улучшить структурирование и управление потоком данных. Мы рассмотрим только случай, когда длина п преобразования распадается в произведение двух взаимно простых множителей п и п . Можно, конечно, применить тот же метод и к большему числу делителей, но тогда число конструктивных возможностей становится необозримым. Например, если ti разлагается в произведение четырех множителей, то из одних и тех же малых БПФ-алгоритмов Винограда можно построить больше чем 10 различных БПФ-алгоритмов Джонсона-Барраса. Чтобы все их проанализировать, необходима специальная процедура поиска типа динамического программирования. Предположим, что л-точечный входной вектор преобразуется в двумерную [п X я )-таблицу V с помощью отображения на расширенную диагональ. Согласно алгоритму Гуда-Томаса для вычисления одномерного преобразования Фурье исходного вектора данных можно сначала вычислить га-точечное преобразование Фурье каждого столбца таблицы, а затем га-точечное преобразование Фурье каждой строки. Эго можно записать в виде V = WWv. Такая запись не является общепринятой, так как v представляет собой двумерную таблицу. Под Wv понимается умножение каждого столбца таблицы v по одному разу на матрицу W, а под W v понимается умножение каждой строки таблицы v по одному раз> на матрицу W . Для,большей строгости надо было бы ввести дополнительные обозначения для отделения матриц, действующих на столбцы, от матриц, действующих на строки; но мы предпочитаем для указания этой информации пользоваться штрихом и двумя штрихами. Так как безразлично, вычисляются ли первыми преобразования по строкам или преобразования по столбцам, то можно также записать V = WWv. Это объясняется тем, что операции по строкам коммутируют с операциями по столбцам, так как такая запись означает ipocTO изменение порядка суммирования. Пред- I---о --1 (о о о о - о с о - о - о о - с о о о - о о с о i- о о о с 0 1С о о о о о о - о о о о - - о с - о о о - о о о I- ° ° 1= о - - ol с - о о - S ; с I---о--о I - о - - с - - о - - о 1~ о о о о о о I locooooo ооссоо-о- а ООООО - ООО 000--0000 а; 3 со-о-оооо ® g с-ооооооо 3 . о о о с. tu -с -1 CQ I S, Ю о о о о о - I о о о о о - о о о о о с: - - о о о о - о о о о о - о с о о о - о о о о о о - - о о о о - о с о о о I- о о о о с о I 1о о -- - - - о1 о - о - - о - о о - - - - о о - о--о - , ПОЛОЖИМ теперь, что имеются малые БПФ-алгоритмы Винограда с W = СВА и W = СВА . Тогда V = (СВА ) (СВА) V = (СВА) (СВА ) V. Две матрицы с одним и тем же количеством штрихов не коммутируют. Однако, как мы видели при исследовании гнездового метода Винограда, матрицы с различным количеством штрихов коммутируют. Для формального доказательства можно обратиться к теореме о кронекеровском произведении матриц. На самом деле, это опять не более чем изменение порядка суммирования. Таким образом, можно записать равенство V = CCBBAA v, которое представляет собой большой БПФ-алгоритм Винограда. Его можно записать также в виде V = CBCB-AA-v. Для построения БПФ-алгоритма Джонсона-Барраса необходима еще одна хитрость. Прежде чем менять порядок следования матриц суммирования, разложим их в виде произведений: W = (GH) В (EF), W = (СН ) В (E F ), где С = GH и так далее. Тогда мы получаем произведение V = GHBEFGH B E F v, которое можно переупорядочить следующим образом: V = (GG H H) (ВВ ) (EE-FF ) v. В этой форме записи обе диагональные матрицы В и В собраны вместе и даже заключены в скобки, чтобы подчеркнуть этот факт. Эти идеи хорошо иллюстрируются 35-точечным преобразованием Фурье. На рис. 8. И выписаны 5-точечный и 7-точечный БПФ-алгоритмы Винограда, каждый из которых состоит из пяти этапов вычислений. Имеется множество способов сочетания их в 35-точечный алгоритм БПФ, наиболее интересные три из которых указаны на рисунке. Два из них соответствуют гнездовому методу Гуда-Томаса и гнездовому методу Винограда. Гнездовой метод Гуда-Томаса приводит к меньшему числу сложений, а гнездовой метод Винограда - к меньшему числу умножений. Надобности выбирать между этими альтернативами, однако, не возникает, так как имеется гнездовой алгоритм Джонсона-Барраса, который содержит столько же умножений, сколько алгоритм Винограда, и число сложений, близкое к числу сложений в алгоритме Гуда-Томаса, и, следовательно, ему надо отдать предпочтение. 8.5. Алгоритмы разложения Малый БПФ-алгоритм Винограда сводит задачу вычисления одномерного преобразования Фурье к задаче вычисления одномерной циклической свертки, используя для этого алгоритм Рейдера. Теперь мы воспользуемся этой же процедурой для многомерных преобразований. В общем случае вычисление преобразования разлагается в вычисление нескольких циклических сверток. Число точек преобразования по каждой из осей многомерного преобразования должно быть равно простому числу или степени простого числа, хотя и не обязательно одной и той же для различных измерений. Сначала, используя вдоль каждой из осей алгоритм Рейдера или его обобщение, сведем многомерное преобразование Фурье к многомерной свертке. Теперь применим алгоритм быстрого вычисления многомерной свертки. Для того случая, когда число точек преобразования вдоль всех осей одно и то же, в разд. 8.7 будет описан алгоритм с лучшими характеристиками, которому и следует отдать предпочтение. Поэтому алгоритмы разложения представляют интерес в первую очередь для тех случаев, когда соответствующие различным осям числа точек преобразования различны. Идея сводится к простому обобщению процедуры для одномерного случая. Начнем с двумерного (п X п )-преобразования Фурье для взаимно простых п и п, возможно, различных: к = 0.....п - 1, к = 0, .... п - I. Для того чтобы воспользоваться алгоритмом Рейдера, надо исключить нуль из показателя степени. Для этого по аналогии с алгоритмом Рейдера разобьем уравнения на четыре группы: V ,o = S Е с. г, Vo.*- - Vo.o = Ёср - 1)°Ё г. г. А = 1.....п - 1, Г-1 г=о Vr. о - Vo.o = Е (ш*- - 1) Е Vr. k=l,..., п ~\, Vr.*--V*., -Vo,t. + Vo.<, = е Ё (<о-*--1)(р--ri Г-о * = 1 , п - 1, г = 1, л 1. Сделав такое разбиение и применив перестановку, даваемую алгоритмом Рейдера, мы сводим задачу к вычислению (л ~ 1)-точеч-ной свертки, (л - 1)-точечной свертки и (га - 1) X (л - 1)-точечной двумерной свертки. Для вычисления обеих одномерных сверток можно воспользоваться построенными в гл. 3 алгоритмами Винограда. Согласно теоремам 4.6.1 и 4.6.2, все умножения в этих алгоритмах являются умножениями только на вещественные или только на мнимые константы, и, следовательно, требуют в случае вещественного входа только по одному вещественному умножению. Для вычисления двумерной свертки можно воспользоваться любым хорошим методом. Одним из них является описанное в гл. 7 полиномиальное преобразование. Алгоритм двумерной ((л - 1) X X (л - 1))-точечной свертки можно также строить гнездовым методом, используя подходящие двумерные циклические свертки меньших объемов или даже малые алгоритмы одномерных циклических сверток. Например, задачу вычисления двумерной (4 X X 12)-свертки можно преобразовать, используя по второй оси алгоритм Агарвала-Кули, в задачу вычисления трехмерной циклической (4х4ХЗ)-свертки. Для решения последней задачи можно воспользоваться гнездовым методом сочетания алгоритма вычисления двумерной циклической (4х4)-свертки с алгоритмом 3-точечной циклической свертки. Если для вычисления двумерного преобразования Фурье используется алгоритм двумерной циклической свертки, то во всех умножениях один из множителей всегда оказывается либо чисто вещественным числом, либо чисто мнимым числом. Частный случай этого утверждения дается следующей теоремой, представляющей собой аналог теоремы 4.6.1. Теорема 8.5.1. Пусть р - нечетное простое число и g (х, у) - многочлен Рейдера от двух переменных степени р - I по каждой из них. Пусть Q (х) и Q (х) - круговые многочлены, делящие х - - 1. Тогда по.модулю Q (х) и по модулю Q (у) коэффициенты многочлена g (х, у) представляют собой либо чисто вещественные числа, либо чисто мнимые чис.ш. Доказательство аналогично доказательству теоремы 4.6.1. и Можно доказать более общую теорему для случая, когда числа точек преобразования по обеим осям равны (не обязательно одинаковым) простым числам или степеням простых чисел. Использование БПФналгоритма Джонсона-Барраса не приводит к каким-либо осложнениям. Все новое, что он привносит, сводится к разбиению сложений на отдельные пакеты, которые можно реализовать в виде отдельных подпрограмм и затем обращаться к ним, вызывая их в нужной последовательности. В процессе вычислений мы постоянно переходим от сложений по строкам к сложениям по столбцам и обратно.
|