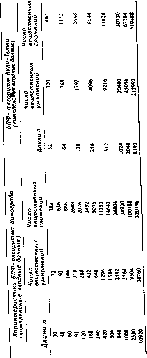применения матриц С и С. (Изменение порядка суммирования оправдано общим тождеством CmECrt-Vri-= Еп- X

X ЕСгй-Кгг.) Тогда

А (я X п ) = пА (л) + М {п ) А (ft).

Теперь мы уже имеем два способа вычисления двумерного преобразования Фурье. Первый из ннх содержит

М (п X п ) = пМ (ft) + пМ (л )

умножений, но строится на основе любого одномерного БПФ-алгоритма, а второй содержит

М (л X л ) = М (л) М (л )

умножений, но в конструкции используются только БПФ-алгоритмы Винограда вдоль каждого из измерений

Например, реализация (1008 х 1008)-преобразования Фурье для комплексного входа в первом случае требует 4X1008X1782 вещественных умножений (см. разд. 8.3), а во втором случае 2х X 1782 вещественных умножений. (В случае вещественного входа во втором случае требуется вдвое меньше вещественных умножений, а в первом случае только 3/4 от указанного числа, так как после применения БПФ-алгоритма по строкам данные становятся комплексными.)

Второй способ, очевидно, лучше, но для его реализации требуется создание временного массива памяти для запоминания комплексных данных объема 2 X 1782 X 1782 (который в начале может содержать 2x1008x1008 входных данных); для первого способа необходима только временная одномерная память для запоминания 3564 слов.

8.3. Алгоритмы Винограда

быстрого вычисления преобразования Фурье большой длины

Гнездовые методы построения двумерных БПФ-алгоритмов можно использовать, наоборот, для построения алгоритмов вычисления одномерного преобразования Фурье. В настоящем разделе мы возвращаемся к задаче вычисления одномерного преобразования Фурье и строим БПФ-алгоритм Винограда для больших длин преобразования (большой БПФ-алгоритм Винограда).

Большой БПФ-алгоритм Винограда представляет собой метод эффективного вычисления дискретного преобразования Фурье, если длина п преобразования распадается в произведение взаимно

вереиндексация на выходе

Рис. 8.5. Переиндексация в 12-то-чечном алгоритме Винограда.

Формирование 12-точечной матрицы преобразования Фурье в виде кронекеровского произведения матриц-составляющих 3-точечного и 4-точечного преобразований Фурье показано на рис. 8.6.

Пусть п ~ пп и W и W обозначают соответственно матрицы п-точечного и -точечного преобразований Фурье, так что V - = Wv и V = W v*, Двумерное {п X гг )-преобразов5ние Фурье двумерного сигнала Vi-i- получается применением W к каждому столбцу сигнала, а затем применением W к каждой строке. Если дву.уерный (п X я ) сигнал vrr был получен описанным переупорядочиванием компонент из одномерного, то надо выполнить обратную перестановку, считывая дву,черный результат по столбцам.

Если под V и V понимать соответственно входной и выходной векторы, компоненты которых переставлены описанным образом, то в терминах кронекеровского произведения преобразование записывается равенством V = (W X W) v. Но W = СВА и W = СВ Л , где элементами матриц А, А , С и С являются только нули и единицы, а матрицы В и В являются диагональными. Так же, как в предыдущем разделе, получаем W = (СВА-) X (СВА) = (С X С) (В X В) (А X А) = СВА,

где кронекеровские произведения С = С X С и А = А X А представляют собой матрицы, состоящие только из нулей и единиц, а кронекеровское произведение В = В X В является диагональной матрицей. Следовательно, мы построили алгоритм я -точечного преобразования Фурье в форме БПФ-алгоритма Винограда: V = CBAv.

При построении алгоритма мы предполагали, что компоненты векторов V и V переупорядочены необходимым образом. Но коль скоро алгоритм в данной фор.ме уже построен, то выполняя тривиальную перестановку столбцов матрицы А, можно работать с естественным порядком компонент вектора v, а переставляя строки матрицы С, - с естественным порядком компонент вектора V.

Обозначим через М (я) и М (л ) размеры матриц В и В соответственно. Эти числа равны числу умножений соответственно в я-точечном БПФ-алгоритме и в л -точечном БПФ-алгоритме с учетом тривиальных у.множенин на единицу. Тогда число умножений, необ.чодимых для выполнения -точечного БПФ-алгоритма Винограда, включая и умножения на единицу, равно М (л) = Л} (я) М (я ). Это происходит потому, что матрица В X В снова является диагональной, а размер ее равен М (я) М (л ).

На рис. 8.7 приведен перечень малых БПФ-алгоритмов Винограда, из которых можно строить большие БПФ-алгоритмы Винограда, а на рис. 8.8 выписаны характеристики больших БПФ-алгоритмов Винограда. На рис. 8.9 дается пример 1008-точечного

nepeuHdeKcaiiufJ на входе ПрОСТЫХ ДбЛИтелеЙ, ДЛЯ КОТОрЫХ

существуют малые БПФ-алгоритмы Винограда. В основу алгоритма заложены четыре самостоятельные идеи: алгоритм Рейдера для простого числа, описанный в разд. 3.4, малый алгоритм свертки Винограда, схема Гуда- Томаса индексации для простых делителей и гнездовой метод Винограда. Большой БПФ-алгоритм Винограда, как видно из рис. 8.4, лучше БПФ-алгоритма Кули-Тьюки по числу умножений, но имеет более сложную структуру. Платой за уменьшение числа операций является отсутствие малых повторяющихся циклов; повторяющиеся циклы имеют большую длину.

в общем случае БПФ-алгоритм Винограда применим для вычисления преобразования, длина п которого равна произведению малых простых чисел или произведению степеней малых простых чисел. Мы рассмотрим только случай двух делителей: п = пп . Используя алгоритм Гуда-Томаса для простых делителей, преобразуем -точечное преобразование Фурье в двумерное (п X X п )-точечное преобразование Фурье. Для вычисления этого двумерного преобразования можно воспользоваться малым п-точечным БПФ-алгоритмом Винограда и малым -точечным БПФ-алгоритмом Винограда, применяя их вдоль соответствующих длине измерений. Вместо этого мы воспользуемся описанным в предыдущем разделе гнездовым методом Винограда, позволяющим так сочетать эти два алгоритма, что число умножений падает.

Рассматриваемая нами процедура иллюстрируется приведенным на рис. 8.5 примером 12-точечного БПФ-алгоритма. На рисунке показано преобразование входного 12-компонентного вектора данных в двумерную таблицу по алгоритму Гуда-Томаса, сводящее задачу к вычислению двумерного преобразования Фурье. За этим следует преобразование полученной двумерной таблицы в новый одномерный массив, формируемый как стек столбцов, (Все эти манипуляции можно проделывать с индексами; совсем не обязательно физически переупорядочивать данные.)

Рис.

изведению.

Вход во

Выход в частотной области

Набор суммирований

Набор умножении\- И

Набор суммирований

Малый БЛФ-алгоритм Винограда Меню

переведение 12-тоне, ого преобразовании Фурье к кроиекеровскому ро-

Умножения Сложения

Рис. 8.7. Набор малых преобразований Винограда.

Число

вещественных умножений

Длинап

Число вещест-

Полнев ьТ-- So e a*

Число нетривиальных умножений на точку *

Число сложений на точку

при комплексном входе удвоить Рис. 8.8. Характеристики больших БПФ-алгоритмов Винограда.